Trang chủ
Lớp 10
Toán Lớp 10 SGK Cũ
Ôn tập chương III - Phương pháp tọa độ trong mặt phẳng
Bài 7 trang 93 SGK Hình học 10
Bài 7 trang 93 SGK Hình học 10
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho đường tròn \((C)\) có tâm \(I(1; 2)\) và bán kính bằng \(3\). Chứng minh rằng tập hợp các điểm \(M\) từ đó ta sẽ được hai tiếp tuyến với \((C)\) tạo với nhau một góc \(60^0\) là một đường tròn. Hãy viết phương trình đường tròn đó.
Hướng dẫn giải
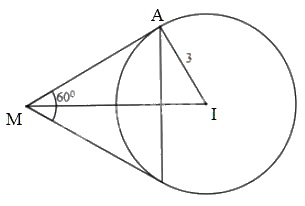
Theo tính chất của tiếp tuyến ta có: \(\widehat {AMI} = {30^0}\)
\(IM = {{IA} \over {\sin \widehat {AMI}}} = {3 \over {\sin {{30}^0}}} = {3 \over {{1 \over 2}}} = 6\)
Gọi tọa độ của \(M\) là \((x ;y)\) Ta có:
\(O{M^2} = {(x - 1)^2} + {(y - 2)^2} = 36\)
Vậy quỹ tích \(M\) là đường tròn tâm \(I (1; 2)\), bán kính \(R = 6\)
Phương trình đường tròn là: \({(x - 1)^2} + {(y - 2)^2} = 36\)
Copyright © 2021 HOCTAP247
