Trang chủ
Lớp 10
Toán Lớp 10 SGK Cũ
Ôn tập chương III - Phương pháp tọa độ trong mặt phẳng
Bài 9 trang 93 SGK Hình học 10
Bài 9 trang 93 SGK Hình học 10
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho elip \((E) = {{{x^2}} \over {16}} + {{{y^2}} \over 9} = 1\) . Tìm tọa độ các đỉnh, các tiêu điểm và vẽ elip đó.
Hướng dẫn giải
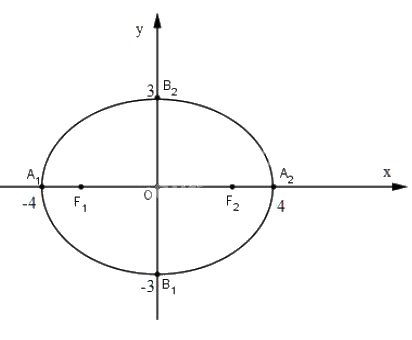
Phương trình chính tắc của Elip \((E) = {{{x^2}} \over {16}} + {{{y^2}} \over 9} = 1\) có dạng là:
\({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\)
Ta có:
\(\eqalign{
& \left\{ \matrix{
{a^2} = 16 \hfill \cr
{b^2} = 9 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = 4 \hfill \cr
b = 3 \hfill \cr} \right. \cr
& c = \sqrt {{a^2} - {b^2}} = \sqrt 7 \cr} \)
+) Tọa độ các đỉnh \(A_1(-4;0), A_2(4; 0), B_1(0; -3)\) và \(B_2(0; 3)\)
+) Tọa độ các tiêu điểm \(F_1(-\sqrt7; 0)\) và \(F_2(\sqrt7; 0)\)
Copyright © 2021 HOCTAP247
