Bài 4 trang 78 SGK Hình học 11

Đề bài

Cho hình bình hành \(ABCD\). Qua \(A, B, C, D\) lần lượt vẽ bốn nửa đường thẳng \(Ax, By, Cz, Dt\) ở cùng phía đối với mặt phẳng \((ABCD)\), song song với nhau và không nằm trong mặt phẳng \((ABCD)\). Một mặt phẳng \((β)\) lần lượt cắt \(Ax, By, Cz\) và \(Dt\) tại \(A', B', C'\) và \(D'\).

a) Chứng minh mặt phẳng \((Ax, By)\) song song với mặt phẳng \(( Cz, Dt)\)

b) Gọi \(I =  AC ∩ BD, J = A'C' ∩ B'D'\). Chứng minh \(IJ\) song song với \(AA'\)

c) Cho \(AA' = a, BB' = b, CC' = c\). Hãy tính \(DD'\).

Hướng dẫn giải

a) Sử dụng định lí: Nếu hai đường thẳng cắt nhau trong mặt phẳng này lần lượt song song với hai đường thẳng trong mặt phẳng kia thì hai mặt phẳng đó song song.

b) Dựa vào định lí: Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau để chứng minh tứ giác \(A'B'C'D'\) là hình bình hành, từ đó suy ra \(J\) là trung điểm của \(A'C'\).

Dựa vào tính chất đường trung bình của hình thang suy ra IJ // AA'.

c) 

Lời giải chi tiết

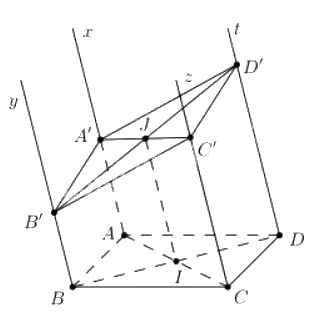
a) \(Ax // Dt\) (giả thiết) và \(AB // CD\) (vì \(ABCD\) là hình bình hành).

Do đó \((Ax, By) // ( Cz, Dt)\)

b) Ta có  \((Ax, By) // ( Cz, Dt)\).

Mặt phẳng \((A'B'C'D')\) lần lượt cắt hai mặt phẳng \((Ax, By)\) và \(( Cz, Dt)\) theo giao tuyến \(A'B'\) và \(C'D'\) \(\Rightarrow A'B'//C'D'\).

Tương tự ta chứng minh được: \(A'D'//B'C'\)

Do đó \(A'B'C'D'\) là hình bình hành.

\(J=A'C'\cap B'D'\) nên \(J\) là trung điểm của \(A'C'\)

Suy ra \(IJ\) là đường trung bình hình thang \(A'C'CA\) do đó \(IJ\) song song với \(AA'\).

c) Chứng minh tương tự ta có \(IJ\) là đường trung bình của hình thang \(BDD'B'\).

Theo tính chất của đường trung bình hình thang ta có:

\(AA'+CC'=2IJ\) và \(BB'+DD'=2IJ\)

Do đó : \(AA'+CC'=BB'+DD' \) \(\Rightarrow DD'=AA'+CC'-BB'\)

\(\Rightarrow DD' = a + c - b\).