Bài 8 trang 80 SGK Hình học 11
Tóm tắt bài
Đề bài
Với giả thiết của bài tập 7, chu vi của thiết diện tính theo \(AM = x\) là:
(A) \(x( 1 + \sqrt3)\);
(B) \(2x ( 1 + \sqrt3)\);
(C) \(3x ( 1 + \sqrt 3)\);
(D) Không tính được.
Hướng dẫn giải
Sử dụng định lí Ta-let tính các cạnh của tam giác \(MNP\).
Lời giải chi tiết
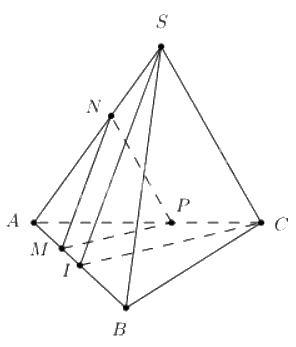
Tam giác ABC đều cạnh \(a \Rightarrow IC = {{a\sqrt 3 } \over 2}\)
Ta có \({{AM} \over {AI}} = {{MP} \over {IC}} = {x \over {{a \over 2}}} = {{2x} \over a}\) \( \Rightarrow MP = {{2x} \over a}.IC = {{2x} \over a}.{{a\sqrt 3 } \over 2} = x\sqrt 3 \)
\( \Rightarrow MP = MN = x\sqrt 3 \)
Áp dụng định lí Ta-let trong tam giác SAC có \({{NP} \over {SC}} = {{AP} \over {AC}} = {{AM} \over {AI}} \Rightarrow NP = SC.{{AM} \over {AI}} = a.{x \over {{a \over 2}}} = 2x\)
Vậy chu vi tam giác MNP bằng \(MN + MP + NP = x\sqrt 3 + x\sqrt 3 + 2x \) \(= 2x\left( {1 + \sqrt 3 } \right)\)
Chọn đáp án B.
Copyright © 2021 HOCTAP247
