Bài 9 trang 114 SGK Hình học 11

Đề bài

Cho hình chóp tam giác đều \(S.ABC \) có \(SH\) là đường cao. Chứng minh \(SA ⊥ BC\) và \(SB ⊥ AC\).  

Hướng dẫn giải

Chứng minh \(BC \bot \left( {SAH} \right);\,\,AC \bot \left( {SBH} \right)\).

Lời giải chi tiết

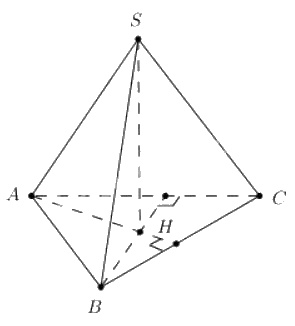
Chóp tam giác đều nên ta có \(H\) là trực tâm của tam giác \(ABC\)

\(SH ⊥ (ABC) \Rightarrow SH ⊥ BC\)

Và \(AH ⊥ BC\) (vì \(H\) là trực tâm)

Suy ra \( BC ⊥ (SAH)\)

\(SA\subset (SAH)\Rightarrow BC ⊥ SA\).

Chứng minh tương tự, ta có:

\(SH \bot \left( {ABC} \right) \Rightarrow SH \bot AC\).

Mà H là trực tâm của tam giác ABC \( \Rightarrow BH \bot AC\)

\( \Rightarrow AC \bot \left( {SBH} \right);\,\,SB \subset \left( {SBH} \right) \Rightarrow AC \bot SB\)