Trọn bộ kiến thức lý thuyết hai mặt phẳng vuông góc chuẩn nhất
Tóm tắt bài
Trong chương trình hình học không gian, hai mặt phẳng vuông góc là kiến thức không thể bỏ qua. Vậy ta tìm hiểu những gì về hai mặt phẳng vuông góc? Trong bài viết cùng bạn đi tìm hiểu về cách chứng minh 2 mặt phẳng vuông góc, tính chất 2 mặt phẳng vuông góc và những bài tập hai mặt phẳng vuông góc.
I) Tìm hiểu chung
Ở phần này, ta đi vào tìm hiểu những nội dung về định nghĩa hai mặt phẳng vuông góc, tính chất 2 mặt phẳng vuông góc và cách chứng minh 2 mặt phẳng vuông góc
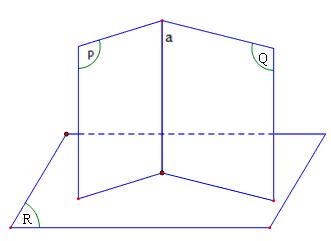
1) Định nghĩa hai mặt phẳng vuông góc
- Góc giữa 2 mặt phẳng bằng \(90^0\) thì hai mặt phẳng đó vuông góc với nhau.
- Cho 2 mặt phẳng (A) và (B) vuông góc với nhau, kí hiệu: \((A) \perp (B)\)
2) Tính chất 2 mặt phẳng vuông góc
- Để hai mặt phẳng vuông góc bắt buộc cần có điều kiện cần và đủ là mặt phẳng (A) phải chứa đường thẳng vuông góc với mặt phẳng (B).
- Bất cứ đường thẳng nào nằm trong mặt phẳng này, vuông góc với giao tuyến thì vuông góc với mặt phẳng kia khi hai mặt phẳng đó vuông góc.
- Cho M là điểm nằm trong (A), đường thẳng d đi qua điểm A và vuông góc với (B) sẽ nằm trong (A) nếu hai mặt phẳng (A) và (B) vuông góc.
- Nếu mặt phẳng (A) và (B) cắt nhau, cùng vuông góc với mặt phẳng thứ 3 thì giao tuyến của (A) và (B) cũng vuông góc với mặt phẳng thứ 3.
- Cho đường thẳng d không vuông góc với mặt phẳng (A) thì có một và chỉ một mặt phẳng (B) vuông góc với mặt phẳng (A).
3) Chứng minh 2 mặt phẳng vuông góc
Để chứng minh 2 mặt phẳng vuông góc với nhau, ta sử dụng các phương pháp sau đây:
3.1) Phương pháp 1
Ta chứng minh mặt phẳng này chứa 1 đường thẳng vuông góc với mặt phẳng kia để suy ra hai mặt phẳng vuông góc với nhau.
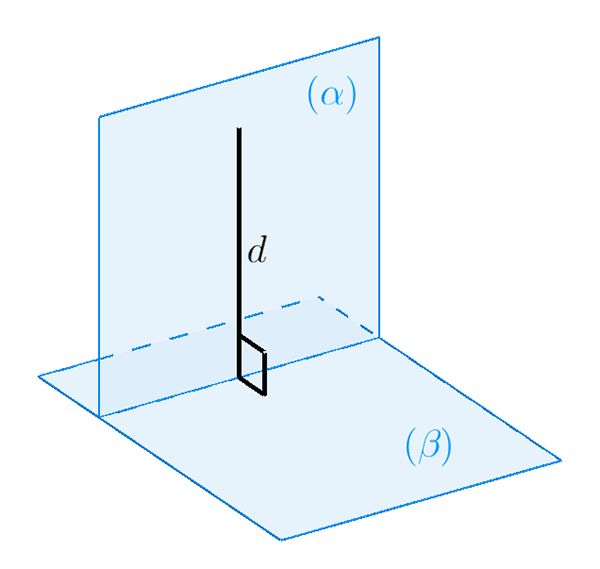
3.2) Phương pháp 2
Ta sử dụng tính chất hai mặt phẳng song song, một mặt phẳng này vuông góc với mặt phẳng thứ 3 thì mặt phẳng kia cũng vuông góc với mặt phẳng thứ 3.
VD: Cho mặt phẳng (A) và (B) song song với nhau, biết rằng (A) vuông góc với mặt phẳng (C). Suy ra (B) vuông góc với (C).
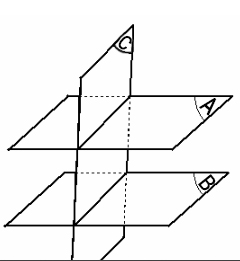
3.3) Phương pháp 3
Giống với phương pháp 2 là ta cũng sử dụng tính chất nhưng phương pháp 3 sử dụng một tính chất khác.
Ta sử dụng tính chất mặt phẳng này vuông góc với một đường thẳng, và đường thẳng đó lại song song với mặt phẳng kia (hoặc đường thẳng nằm trong mặt phẳng kia) thì hai mặt phẳng đó song song với nhau.
VD: Mặt phẳng (A) vuông góc với đường thẳng d, mặt phẳng (B) vuông góc với d (hoặc chứa d) thì (A) và (B) vuông góc với nhau.
II) Luyện tập
Tại phần luyện tập gửi đến bạn một số bài tập hai mặt phẳng vuông góc giúp bạn củng cố kiến thức ở phía trên.
Bài tập 1: Cho hình tứ diện SABC, \(SA \perp (ABC)\). AE và CF là đường cao cắt nhau tại O trong tam giác ABC. Biết thêm trọng tâm tam giác SBC là H.
Chứng minh rằng: 1) \((SBC) \perp (SAE)\), \((SBC) \perp (CFH)\)
2) \(OH \perp (SBC)\)
Hướng dẫn
Sử dụng các số liệu đề bài cho cùng với áp dụng linh hoạt tính chất và phương pháp chứng minh hai mặt phẳng vuông góc ở phía trên phần tìm hiểu chung.
1) Ta có: \(BC \perp AE, BC \perp SE\) ⇒ \(BC \perp (SAE)\), BC nằm trong (SBC) nên suy ra \((SAE) \perp (SBC)\)
\(SA \perp (ABC)\) ⇒ \(CF \perp SB\) (1)
H là trọng tâm tam giác SBC, suy ra \(CH \perp SB\) (2)
Từ (1) và (2) suy ra \(SB \perp (CFH)\), \(SB \subset (SBC)\)
Suy ra: \((SBC) \perp (CFH)\)
2) Từ phần chứng minh câu 1, ta suy ra được \(BC \perp OH\) và \(SB \perp OH\)
Bài tập 2: Cho hình chóp SABCD có đáy là hình vuông. Biết rằng SAB là tam giác đều và vuông với mặt phẳng ABCD.
Chứng minh rằng \((SAB) \perp (SAD), (SAB) \perp (SBC)\)
Hướng dẫn
Gọi G là chung điểm của AB.
- Có: SAB là tam giác đều nên \(SH \perp AB\)
\((SAB) \perp (ABCD) \), hai mặt phẳng giao nhau tại AB
Suy ra, \(SH \perp (ABCD) => SH \perp AD\) (1)
- S.ABCD có đáy là hính vuông nên \(AB \perp AD\) (2)
Kết hợp (1) và (2), suy ra \(AD \perp (SAB)\) mà AD thuộc mặt phẳng (SAD).
Suy ra, \((SAB) \perp (SAD)\)
- Chứng minh tương tự ta có \((SAB) \perp (SBC)\)
Xem thêm>>> Giải bài tập SGK
Trên đây là bài viết tổng hợp được về kiến thức lý thuyết hai mặt phẳng vuông góc. Hy vọng sau bài viết các bạn có thể nắm được tính chất 2 mặt phẳng vuông góc, cách chứng minh 2 mặt phẳng vuông góc và cách giải bài tập hai mặt phẳng vuông góc. Chúc các bạn học tập tốt
Copyright © 2021 HOCTAP247