Bài 3 trang 119 SGK Hình học 11

Đề bài

Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Chứng minh rằng các khoảng cách từ các điểm \(B, C, D, A', B', D'\) đến đường chéo \(AC'\) đều bằng nhau. Tính khoảng cách đó.

Hướng dẫn giải

+) Xác định và tính khoảng cách từ điểm B đến AC' bằng cách sử dụng hệ thức lượng trong tam giác vuông.

+) Chứng minh các tam giác bằng nhau và suy ra các đường cao tương ứng bằng nhau.

Lời giải chi tiết

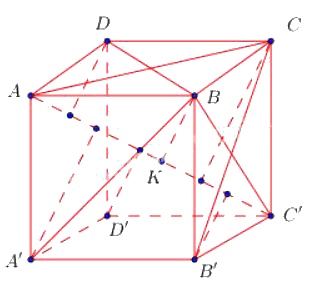
Gọi \(K\) là hình chiếu của \(B\) trên \(AC'\). 

Ta có \(AB \bot \left( {BCC'B'} \right) \Rightarrow AB \bot BC' \Rightarrow \Delta ABC'\) vuông tại B.

Dễ thấy \(BC'\) là đường chéo của hình vuông cạnh \(a \Rightarrow BC' = a\sqrt 2 .\)

Áp dụng hệ thức lượng trong tam giác vuông \(ABC'\) có: 

\(\frac{1}{BK^{2}}=\frac{1}{BA^{2}}+\frac{1}{BC^{2}}=\frac{1}{a^{2}}+\frac{1}{(a\sqrt{2})^{2}}=\frac{3}{2a^{2}}\)\( \Rightarrow BK=\frac{a\sqrt{6}}{3}.\) 

Ta có:

\(\Delta ABC' = \Delta C'CA = \Delta ADC' \)\(= \Delta AA'C' = \Delta C'B'A = \Delta C'D'A\)

\((c.g.c)\)

Do đó các chiều cao tương ứng của các tam giác bày bằng nhau, chứng tỏ khoảng cách từ \(B, C, D, A', B', D'\) tới \(AC'\) đều bằng \( \frac{a\sqrt{6}}{3}\).