Bài 6 trang 119 SGK Hình học 11
Tóm tắt bài
Đề bài
Chứng minh rằng nếu đường thẳng nối trung điểm hai cạnh \(AB\) và \(CD\) của tứ diện \(ABCD\) là đường vuông góc chung của \(AB\) và \(CD\) thì \(AC = BD\) và \(AD = BC\).
Hướng dẫn giải
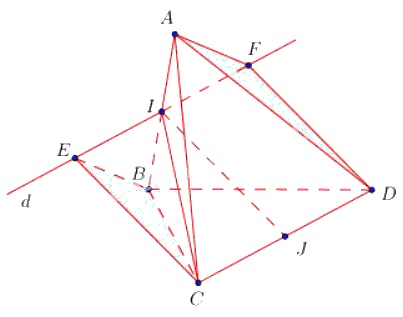
Qua \(I\) kẻ đường thẳng \(d // CD\), lấy trên \(d\) điểm \(E, F\) sao cho \(IE = IF = \frac{CD}{2}\)
Ta có \(IJ // CD\,\, (gt) \Rightarrow IJ // EF\), lại có \(IJ // AB \,\,(gt)\)
\(\Rightarrow IJ \bot (AEBF)\).
Ta có \(CDFE\) là hình bình hành có \(IJ\) là đường trung bình
\( \Rightarrow CE // DF // IJ\)
\( \Rightarrow \left\{ \begin{array}{l}CE \bot \left( {AEBF} \right) \Rightarrow CE \bot BE\\DF \bot \left( {AEBF} \right) \Rightarrow DF \bot AF\end{array} \right.\)
Ta có: \(\Delta AIF = \Delta BIE(c.g.c)\) suy ra: \(AF=BE\)
Xét \(∆DFA\) và \(∆CEB\) có:
+) \(\widehat E = \widehat F( = {90^0})\)
+) \(AF=BE\)
+) \(DF=CE\)
\(\Rightarrow ∆DFA=∆CEB(c.g.c) \Rightarrow AD = BC\).
Chứng minh tương tự ta được \(BD = AC\).
Copyright © 2021 HOCTAP247
