Bài 8 trang 120 SGK Hình học 11
Tóm tắt bài
Đề bài
Cho tứ diện đều \(ABCD\) cạnh \(a\). Tính khoảng cách giữa hai cạnh đối diện của tứ diện.
Hướng dẫn giải
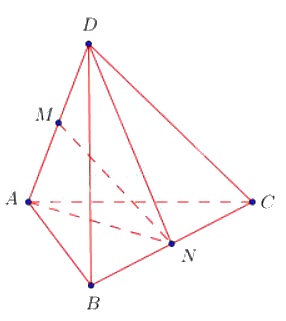
Gọi \(M, N\) lần lượt là trung điểm của \(AD\) và \(BC\),
Ta có: \(\Delta BAC = \Delta BDC(c.c.c)\) \( \Rightarrow AN = DN\) (hai đường trung tuyến tương ứng)
\(\Rightarrow \Delta AND\) cân tại \(N\).
\(\Rightarrow\) Trung tuyến \(MN\) đồng thời là đường cao \(\Rightarrow MN\bot AD \,\,\, (1)\)
Chứng minh tương tự, \(\Delta MBC\) cân tại \(M \Rightarrow MN\bot BC \,\,\,\,\, (2)\)
Từ (1) và (2) suy ra \(MN\) là đường vuông góc chung của \(BC\) và \(AD\).
\( \Rightarrow d\left( {AD;BC} \right) = MN\)
Tam giác \(ABC\) đều cạnh \(a\) nên \(AN={{a\sqrt 3 } \over 2}\)
Áp dụng định lí Pytago vào tam giác vuông \(AMN\) ta có:
\(MN = \sqrt {A{N^2} - A{M^2}} = \sqrt {{{3{a^2}} \over 4} - {{{a^2}} \over 4}} = {{a\sqrt 2 } \over 2}\).
Vậy \(d\left( {AD;BC} \right) = \frac{{a\sqrt 2 }}{2}\).
Copyright © 2021 HOCTAP247
