Lý thuyết về khoảng cách Toán 11

Lý thuyết về khoảng cách Toán 11

Bài viết dưới đây  sẽ giúp các bạn làm sáng tỏ nội dung lý thuyết về Toán hình 11 Khoảng cách!

I. Lý thuyết?

1. Định nghĩa

- Để tìm khoảng cách giữa một điểm tới một mặt phẳng ta xét khoảng cách giữa M tới điểm H thuộc mặt phẳng ban đầu, Khi đó H sẽ được gọi là hình chiếu của điểm M tới mặt phẳng.

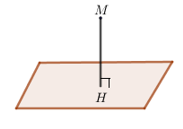
Kí hiệu: \(d(M,(P))=MH\)

2. Từ một điểm cho tới mặt phẳng

Phương pháp:

Ta  áp dụng cách làm cho khoảng cách từ một điểm bất kỳ đến đường thẳng là từ đường thẳng ta kẻ một góc vuông với mặt phẳng. Từ đó ta xác định được hình chiếu của điểm đó trên mặt phẳng. Tính khoảng cách từ điểm cần tính đến hình chiếu ta được độ dài cần tìm.

TH1:

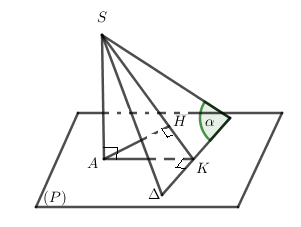
- Dựng \(AK⊥Δ⇒Δ⊥(SAK)⇒(α)⊥(SAK)\) và \((α)∩(SAK)=SK\)

- Dựng \(AH⊥SK⇒AH⊥(α)⇒d(A,(α))=AH\)

TH2:

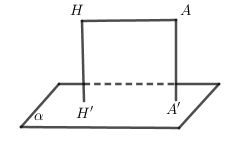
- Tìm điểm \(H∈(α)\) sao cho \(AH//(α)⇒d(A,(α))=d(H,(α))\)

TH3:

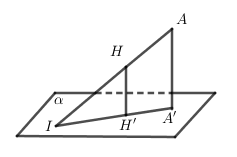
- Tìm điểm H sao cho \(AH∩(α)=I\)

- Khi đó: \(d(A,(α))=IAIH⇒d(A,(α))=IA\).

Giải toán 11 khoảng cách

II. Các bài toán về khoảng cách lớp 11

+ Dạng 1: Khoảng cách từ 1 điểm đến đường thẳng

Việc dựng hình chiếu của một điểm trên đường thẳng trong không gian, ta có thể làm theo 2 cách sau:

+ Dựng mặt phẳng đi qua điểm và đường thẳng đã cho. Rồi trên mặt phẳng đó qua điểm đã cho dựng đoạn vuông góc từ điểm tới đường thẳng.

+ Dựng một mặt phẳng đi qua điểm đã cho và vuông góc với đường thẳng, lúc đó giao điểm của đường thẳng với mặt phẳng vừa dựng chính là hình chiếu của điểm trên đường thẳng.

Sau khi đã xác định được khoảng cách cần tính, ta dùng các hệ thức lượng trong tam giác, đa giác, đường tròn … để tính toán.

+ Dạng 2: Từ điểm bất kỳ cho tới mặt phẳng xác định

Ví dụ: Xét hình S.ABCD ta có ABCD là hình vuông. Với một điểm S bất kỳ ta xác định một hình chiếu xuống đáy của tứ giác. Yêu cầu tính khoảng cách từ S cho tới đáy, biết rằng góc SAC bằng 30 độ?

Chứng minh \(DB\bot (SAC)\) suy ra hình chiếu vuông góc của DS lên (SAC) là SO, góc giữa SD và (SAC) là \(DSO=30^0\). Đặt DO=x, ta có \(SO=x\sqrt3\) (O là giao điểm của AC và BD).

Từ đó \(SO^2=AO^2+SA^2\Rightarrow x=\dfrac{a}{\sqrt2}\).

Gọi N là trung điểm của AB suy ra DN//BM.

Suy ra \(d(D;(SBM))=d(N;(SBM))=\dfrac{1}{2}d(A;(SBM))\)

Kẻ \(AI\bot BM, AH\bot SM\).

Từ đó chứng minh được \(AH\bot (SBM) \Rightarrow d(A;(SBM))=AH\)

Trong (ABCD): \(S_{ABM}=S_{ABCD}-S_{BCM}=\dfrac{a^2}{2}\)

Mà \(S_{ABM}=\dfrac{1}{2}AI.BM=> AI=\dfrac{2a}{\sqrt5}\).

Khi đó: \(\dfrac{1}{AH^2}=\dfrac{1}{AI^2}+\dfrac{1}{SA^2}\Rightarrow AH=\dfrac{2}{3}a\Rightarrow d(D;(SBM)=\dfrac{a}{3}\).

+ Dạng 3: Khoảng cách giữa hai mặt phẳng song song

Việc tính khoảng cách giữa một đường thẳng và một mặt phẳng song song với nó, hoặc tính khoảng cách giữa hai mặt phẳng song song đều quy về việc tính khoảng cách từ điểm đến mặt phẳng. Cần lưu ý việc chọn điểm trên đường hoặc trên

mặt sao cho việc xác định khoảng cách được đơn giản nhất.

III. Bài tập vận dụng

Bài 1: Trong mặt phẳng cho sẵn P và Q ta có các mặt bên vuông góc với nhau, lấy giao tuyến tại là đường thẳng d. Lần lượng lấy theo thứ tự hai điểm A và B sao cho khoảng cách giữa hai điểm này tạo thành một đường thẳng có độ dài tổng quát là a. Tiếp theo ta chọn hai điểm C và D nằm trên từng mặt phẳng P và Q sao cho chúng thỏa mãn điều kiện AC vuông góc với BD. Tìm d giữa A và mặt phẳng BCD.

Lời giải:

Ta có \((P)\bot(Q),(P)\cap(Q) =d,AC\in (P)\),

\(AC\bot d\Rightarrow AC\bot(Q)\Rightarrow BD\bot AC.\)

Lại có \(BD\bot AB\Rightarrow BD\bot (ABC)(1)\)

Gọi H là chân đường vuông góc hạ từu A xuống BC. Theo giả thiết cho rằng tam giác ban đầu sau khi thêm các đường vuông cân tại A nên ta có điều luôn đúng: \(AH\bot BC\) và \(AH=\dfrac{BC}{2}=\dfrac{a\sqrt2}{2}\).

Bài 2: SA=3a là cạnh của hình chóp S.ABC và \(SA\bot(ABC)\). Giả sử AB=BC=2a, góc ABC=120 độ. d(A, (SBC)) bằng bao nhiêu?

Lời giải:

Dựng \(AD\bot BC(D\in BC) \ và \ AH\bot SD(H\in SD).\)

Theo điều kiện cho sẵn của đầu bài ta có \(CD\bot SA, CD\bot AD\) (do dựng)

\(\Rightarrow CD\bot (SAD)\Rightarrow AH\bot CD\), mà \(AH\bot SD \Rightarrow AH\bot (SCD)\) AH vuông góc lên (SBC).

Ta có \(AD=AB.sin\widehat {ABD}=2asin60^0=a\sqrt3\).

Với những gì mà đã giúp các bạn khái quát nội dung về toán khoảng cách lớp 11 trên đây, hy vọng sẽ giúp các bạn đạt kết quả cao trong học tập!