Tổng hợp phương pháp chứng minh ba điểm thẳng hàng - Không thể bỏ qua
Tóm tắt bài
PHƯƠNG PHÁP CHỨNG MINH BA ĐIỂM THẲNG HÀNG
Bộ môn Toán 7 các em học sinh cần nhớ Các cách chứng minh ba điểm thẳng hàng. Nội dung này rất quan trọng vì vận dụng nhiều bài Hình học khác. Sau đây cunghocvui.com sẽ tổng hợp kiến thức về phần này.
1. Sử dụng tiên đề Ơclit
Cho 2 đoạn thẳng, trong đó 1 đoạn thẳng tạo thành từ 3 điểm đã cho cùng song song với 1 đường thẳng.
Ví dụ:
.png)
AM//xy, BM//xy => A, M, B thẳng hàng (theo tiên đề Ơclit).
2. Sử dụng tính chất góc bẹt
Nếu cùng tạo với nhau thành 1 góc có \(180^o\) thì 3 điểm thẳng hàng.
Ví dụ:
.png)
Ta thấy \(\widehat{ABC} = 180^o\) => A, B, C thẳng hàng.
3. Sử dụng tính chất đường trung trực của một đoạn thẳng
Nếu 3 điểm đều cùng thuộc đường trung trực của đoạn thẳng nào đó thì 3 điểm thẳng hàng.
Ví dụ:
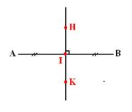
Sau khi chứng minh H, I, K cùng thuộc đường trung trực của AB => H, I, K thẳng hàng.
4. Sử dụng tính duy nhất của tia phân giác của một góc khác góc bẹt
Mỗi một góc bẹt chỉ có 1 tia phân giác duy nhất.
Ví dụ:
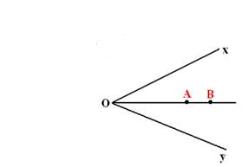
OA, OB đều là tia phân giác của \(\widehat{xOy}\).
=> A, O, B thẳng hàng
5. Sử dụng tính chất hai đường thẳng vuông góc
3 điểm đã cho cùng vuông góc với 1 đường thẳng nào đó.
Ví dụ:
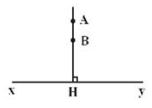
Ta có: AH \(\perp \) \(xy\), BH \(\perp \) \(xy\) => A, H, B thẳng hàng.
6. Sử dụng tính chất các đường đồng quy của tam giác
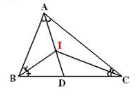
Sau khi chứng minh I là trọng tâm của tam giác ABC, AD là trung tuyến của tam giác ABC
=> A, I, D thẳng hàng.
Sau khi học xong các phương pháp chứng minh ba điểm thẳng hàng, có thể tham khảo các dạng bài tập.
Copyright © 2021 HOCTAP247
