Hình học 9 Bài 1: Góc ở tâm và số đo cung
Tóm tắt bài
1.1. Góc ở tâm
ĐỊNH NGHĨA: Góc có đỉnh trùng với tâm của đường tròn được gọi là góc ở tâm.
.png)
- Cung nằm bên trong góc gọi là cung bị chắn, góc AOB chắn cung nhỏ \(\stackrel\frown{AmB}\) .
- Trong trường hợp hình số 2, góc bẹt COD chắn nửa đường tròn.
1.2. Số đo cung
ĐỊNH NGHĨA
- Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
- Số đo của cung lớn bằng hiệu giữa 3600 và số đo của cung nhỏ (có chung 2 mút với cung lớn).
- Số đo của nửa đường tròn bằng 1800.
Kí hiệu: số đo cung AB là sđ\(\stackrel\frown{AB}\).
CHÚ Ý:
- Cung nhỏ có số đo nhỏ hơn 1800.
- Cung lớn có số đo lớn hơn 1800.
- Khi hai mút của cung trùng nhau, ta có "cung không" với số đo 00 và cung cả đường tròn có số đo 3600.
1.3. So sánh hai cung
Trong cùng một đường tròn hay hai đường tròn bằng nhau:
- Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.
- Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.
1.4. Khi nào thì sđ\(\stackrel\frown{AB}\) = sđ\(\stackrel\frown{AC}\) + sđ\(\stackrel\frown{CB}\)?
ĐỊNH LÍ: Nếu C là một điểm trên cung AB thì: sđ\(\stackrel\frown{AB}\) = sđ\(\stackrel\frown{AC}\) + sđ\(\stackrel\frown{CB}\).png)
2.1. Bài tập cơ bản
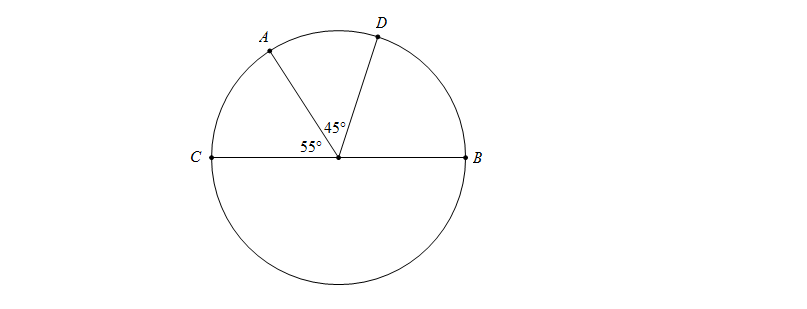
Bài 1: Dựa vào hình vẽ sau, hãy tính số đo cung AB:
.png)
Hướng dẫn: Theo định nghĩa ta có sđ\(\stackrel\frown{BC}=30^{0}\), sđ\(\stackrel\frown{AC}=45^{0}\)
Mà điểm C nằm trên cung AB nên sđ\(\stackrel\frown{AB}\)=sđ\(\stackrel\frown{AC}\)+sđ\(\stackrel\frown{BC}\)\(=45^0+30^0=75^0\)
Bài 2: Dựa vào hình vẽ sau, hãy tính số đo cung nhỏ BC:
.png)
Hướng dẫn: \(\bigtriangleup OAC\) có \(OA=OC\) nên \(\bigtriangleup OAC\) cận tại \(O\), suy ra \(\widehat{AOC}=180^0-2\widehat{OAC}=180^0-2.30^0=120^0\).
Khi đó, số đo cung lớn BC là: sđ\(\stackrel\frown{BC}\)lớn \(=110^0+120^0=230^0\).
Suy ra sđ\(\stackrel\frown{BC}\)nhỏ\(=360^0-\)sđ\(\stackrel\frown{BC}\)lớn \(=360^0-230^0=130^0\)
Vậy số đo cung nhỏ BC là \(130^0\).
Bài 3: Cho đường tròn tâm O, đường kính BC. A là điểm thuộc đường tròn sao cho \(\widehat{AOC}=75^0\). So sánh số đo hai cung nhỏ AC và AB:
.png)
Hướng dẫn: Ta có \(\widehat{AOC}+\widehat{AOB}=180^0\Rightarrow \widehat{AOB}=180^0-\widehat{AOC}=180^0-75^0=105^0\).
Từ đó suy ra sđ\(\stackrel\frown{AC}=75^0\), sđ\(\stackrel\frown{AB}=105^0\) nên sđ\(\stackrel\frown{AB}\)>sđ\(\stackrel\frown{AC}\).
2.2. Bài tập nâng cao
Bài 1: Cho hình vẽ sau:
.png)
Tính số đo cung nhỏ AB, \(\widehat{ADB}\) từ đó so sánh hai cạnh AC và AD.
Hướng dẫn: \(\bigtriangleup ACO\) vuông tại A có \(\widehat{ACO}=20^0\) nên \(\widehat{AOC}=90^0-20^0=70^0\Rightarrow\)sđ\(\stackrel\frown{AB}=70^0\)
\(\widehat{AOB}\) là góc ngoài của tam giác cân AOD. Nên \(\widehat{ADB}=\frac{1}{2}\widehat{AOB}=\frac{1}{2}.70^0=35^0\).
Xét \(\bigtriangleup ACD\) có \(\widehat{ACD}<\widehat{ADC}(20^0<35^0)\) nên \(AC>AD\).
Bài 2: Dựa vào hình dưới, hãy tính số đo cung nhỏ AB, biết rằng B là trung điểm OC.
.png)
Hướng dẫn: Tam giác ABC vuông tại A có B là trung điểm OC nên BO=BC=BA.
Mà OB=OA suy ra OB=OA=AB, từ đó \(\bigtriangleup OAB\) đều. Lúc đó \(\widehat{AOB}=60^0\) nên số đo cung nhỏ AB là \(60^0\).
3. Luyện tập Bài 1 Chương 3 Hình học 9
Qua bài giảng Góc ở tâm và số đo cung này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :
- Nắm vững các định nghĩa góc ở tâm, số đo cung
- Biết cách so sánh hai cung
3.1 Trắc nghiệm về Góc ở tâm và số đo cung
Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 9 Bài 1 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
- A. 4
- B. 2
- C. 1
- D. 3
-
- A. sđ\(\stackrel\frown{BD}=80^0\) và sđ\(\stackrel\frown{AB}\) > sđ\(\stackrel\frown{CD}\)
- B. sđ\(\stackrel\frown{BD}=80^0\) và sđ\(\stackrel\frown{AB}\) < sđ\(\stackrel\frown{CD}\)
- C. sđ\(\stackrel\frown{BD}=85^0\) và sđ\(\stackrel\frown{AB}\) > sđ\(\stackrel\frown{CD}\)
- D. sđ\(\stackrel\frown{BD}=85^0\) và sđ\(\stackrel\frown{AB}\) < sđ\(\stackrel\frown{CD}\)
Câu 2- Câu 5: Xem thêm phần trắc nghiệm để làm thử Online
3.2 Bài tập SGK về Góc ở tâm và số đo cung
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 9 Bài 1 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Toán 9 tập 1
Bài tập 1 trang 68 SGK Toán 9 Tập 2
Bài tập 2 trang 69 SGK Toán 9 Tập 2
Bài tập 3 trang 69 SGK Toán 9 Tập 2
Bài tập 4 trang 69 SGK Toán 9 Tập 2
Bài tập 5 trang 69 SGK Toán 9 Tập 2
Bài tập 6 trang 69 SGK Toán 9 Tập 2
Bài tập 7 trang 69 SGK Toán 9 Tập 2
Bài tập 8 trang 70 SGK Toán 9 Tập 2
Bài tập 9 trang 70 SGK Toán 9 Tập 2
Bài tập 3 trang 99 SBT Toán 9 Tập 2
4. Hỏi đáp Bài 1 Chương 3 Hình học 9
Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HOCTAP247 sẽ sớm trả lời cho các em.
Copyright © 2021 HOCTAP247