(4,0 điểm)        Cho tam giác ABC có ba góc nhọn và AB > AC. Tam giác ABC nội tiếp đường tròn (O; R). Đường cao AH của tam giác ABC cắt đường tròn (O; R) tại đ...

Câu hỏi :

(4,0 điểm)        Cho tam giác ABC có ba góc nhọn và AB > AC. Tam giác ABC nội tiếp đường tròn (O; R). Đường cao AH của tam giác ABC cắt đường tròn (O; R) tại điểm thứ hai là D. Kẻ DM vuông góc với AB tại M.a) Chứng minh tứ giác BDHM nội tiếp đường tròn.b) Chứng minh DA là tia phân giác của 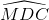c) Gọi N là hình chiếu vuông góc của D lên đường thẳng AC, chứng minh ba điểm M, H, N thẳng hàng.d) Chứng minh  AB² + AC² + CD² + BD²  = 8R²