Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 9cm, HC = 16cm

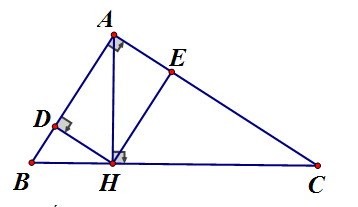
    a)     Áp dụng hệ thức lượng vào $\Delta ABC$ vuông tại A, AH đường cao

$\Rightarrow A{H}^2=BH.HC$ hay $A{H}^2=9.16=144\Rightarrow AH=\sqrt{144}=12\left(cm\right)$

Áp dụng định lý Pytago vào các tam giác vuông AHB, AHC có:

Vậy $AH=12cm,AB=15cm,AC=20cm$

     b)    Tứ giác ADHE có $\widehat{A}=\widehat{D}=\widehat{E}={90}^0\Rightarrow ADHE$ là hình chữ nhật

      c) $\Delta AHB$ vuông tại H, HE là đường cao $\Rightarrow AD.AB=A{H}^2$ (hệ thức lượng)

Hay $AD.15={12}^2\Rightarrow AD=9,6\left(cm\right)$

$\Delta AHC$ vuông tại H, HE là đường cao nên $AE.AC=A{H}^2$ (hệ thức lượng)

Hay $AE.20={12}^2\Rightarrow AE=7,2cm$

Chu vi tứ giác $ADHE=2.\left(AD+AE\right)=2.\left(9,6+7,2\right)=33,6\left(cm\right)$