Cho hình thoi ABCD cạnh a. Gọi R và r lần lượt là bán kính các đường tròn

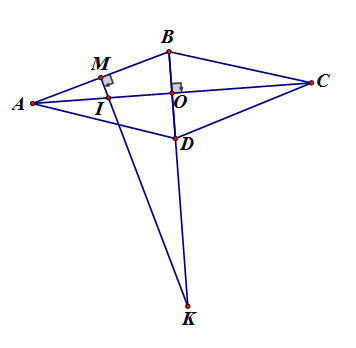
Gọi M, I, K là giao điểm của đường trung trực AB với AB, AC, BD, O là giao điểm của AC và BD.

Ta có: $OA=OC,OB=OD,AC\perp BD$(Vì ABCD là hình thoi)

Nên AC là trung trực của BD, BD là trung trực của AC

Do đó I, K lần lượt là tâm đường tròn ngoại tiếp $\Delta ADB,\Delta ABC$ $\Rightarrow IA=R,KB=r$

Xét $\Delta OAB$ và $\Delta MKB$ có $\widehat{ABO}$ chung, $\widehat{AOB}=\widehat{KMB}\left(={90}^0\right)$

Do đó: $\Delta OAB~\Delta MKB$

$\Rightarrow \frac{OB}{MB}=\frac{AB}{KB}\Rightarrow \frac{OB}{\frac{a}{2}}=\frac{a}{r}\Rightarrow O{B}^2={\left(\frac{a^2}{2r}\right)}^2=\frac{a^4}{4r^2}$

Tương tự ta có: $O{A}^2=\frac{a^2}{4R^2}$

$\Delta OAB$ vuông tại O, theo định lý Pytago ta có:

$O{A}^2+O{B}^2=A{B}^2\Rightarrow \frac{a^4}{4R^2}+\frac{a^4}{4R^2}=a^2\Rightarrow \frac{1}{R^2}+\frac{1}{r^2}=\frac{4}{a^2}\left(dfcm\right)$