Cho đường tròn (O) bán kính OA, dây CD là đường trung trực của OA

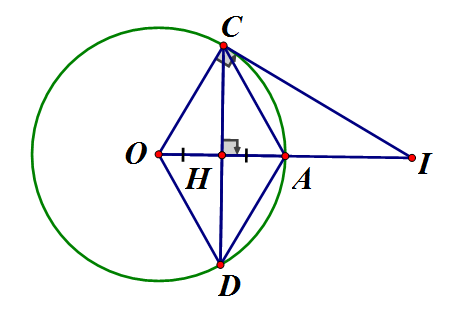
a) Ta có: $OH\perp CD$ tại  $H\left(H=OA\cap CD\right)\Rightarrow H$ là trung điểm CD

Tứ giác OCAD có hai đường chéo CD và OA vuông góc nhau tại trung điểm mỗi đường nên OCAD là hình thoi

b) Ta có: H là trung điểm $OA\Rightarrow OH=\frac{1}{2}OA=\frac{R}{2}$

Áp dụng định lý Pytago vào $\Delta OHC$ vuông tại H, ta có:

$CH=\sqrt{O{C}^2-O{H}^2}=\sqrt{R^2-\frac{R^2}{4}}=\frac{R\sqrt{3}}{2}$

$\Delta OCI$ vuông tại C, CH đường cao, áp dụng hệ thức lượng ta có:

$\frac{1}{C{H}^2}=\frac{1}{C{O}^2}+\frac{1}{C{I}^2}hay\frac{1}{{\left(\frac{R\sqrt{3}}{2}\right)}^2}=\frac{1}{R^2}+\frac{1}{C{I}^2}$

$\Rightarrow \frac{1}{C{I}^2}=\frac{4}{3R^2}-\frac{1}{R^2}=\frac{1}{3R^2}\Rightarrow CI=\sqrt{3R^2}=R\sqrt{3}$