Cho nửa đường tròn (O) đường kính AB. Kẻ hai tiếp tuyến Ax, By (Ax, By

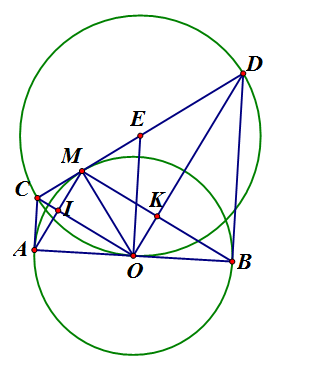
a) Vì CM, CA là hai tiếp tuyến cắt nhau nên $\widehat{MOC}=\widehat{AOC}=\frac{1}{2}\widehat{AOM}$

Chứng minh tương tự $\Rightarrow \widehat{MOD}=\widehat{DOB}=\frac{1}{2}\widehat{MOB}$

$\Rightarrow \widehat{COD}=\widehat{COM}+\widehat{MOD}=\frac{1}{2}\left(\widehat{AOM}+\widehat{MOB}\right)$$=\frac{1}{2}\widehat{AOB}=\frac{1}{2}{.180}^0={90}^0$

Vậy $\widehat{COD}={90}^0$

b) Cũng theo tính chất hai tiếp tuyến cắt nhau $\Rightarrow OC$ là trung trực của AM $\Rightarrow \widehat{I}={90}^0$

Chứng minh tương tự $\Rightarrow \widehat{K}={90}^0$

Tứ giác MIOK có $\widehat{COD}=\widehat{I}=\widehat{K}={90}^0\Rightarrow OIMK$ là hình chữ nhật

c) Theo tính chất hai tiếp tuyến cắt nhau $\Rightarrow \left\{\begin{array}{l}AC=MC\\ BD=MD\end{array}\right.\Rightarrow AC.MD=MC.MD$

Áp dụng hệ thức lượng vào $\Delta COD$ vuông tại O, OM đường cao $\Rightarrow MC.MD=O{M}^2=R^2$

Vậy $AC.BD=R^2$ không đổi .

d) Gọi E là trung điểm CD. Ta có CA // DB (cùng vuông góc với $AB)\Rightarrow CABD$ là hình thang có E là trung điểm CD, O là trung điểm $AB\Rightarrow EO$ là đường trung bình hình thang $CABD\Rightarrow EO\perp AB$ và OE = OC = OD (tính chất đường trung tuyến ứng với cạnh huyền)$\Rightarrow O\in \left(E;ED\right)$ và $EO\perp AB$ nên AB là tiếp tuyến của (E)