Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Bài tập theo tuần Toán 9 - Tuần 14 !!
Cho tam giác nhọn ABC có AD, BE, CF là...
Cho tam giác nhọn ABC có AD, BE, CF là ba đường cao cắt nhau tại H. M, N
Câu hỏi :
Cho tam giác nhọn ABC có AD, BE, CF là ba đường cao cắt nhau tại H. M, N lần lượt là hình chiếu của B, C trên đường thẳng EF. Chứng minh rằng:
a)
b) H là tâm đường tròn nội tiếp
c) A, B, C là tâm đường tròn bàng tiếp của
d)
Cho tam giác nhọn ABC có AD, BE, CF là ba đường cao cắt nhau tại H. M, N lần lượt là hình chiếu của B, C trên đường thẳng EF. Chứng minh rằng:
a)
b) H là tâm đường tròn nội tiếp
c) A, B, C là tâm đường tròn bàng tiếp của
d)
* Đáp án
* Hướng dẫn giải
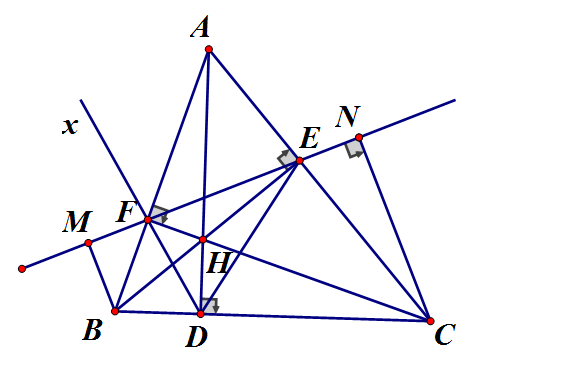
a) Xét và có chung;
Xét và có: chung;
b)
cmtt
Ta có nên là đường phân giác của . Chứng mnh tương tự ta cũng có DH là đường phân giác là tâm đường tròn nội tiếp
c) Gọi Fx là tia đối của tia FD
Ta có: mà , do đó
A là giao điểm của đường phân giác và đường phân giác ngoài đỉnh F nên A là tâm đường tròn bàng tiếp trong góc D của Chứng minh tương tự ta cũng có B, C là tâm đường tròn bàng tiếp
d) Theo bài
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập theo tuần Toán 9 - Tuần 14 !!
Số câu hỏi: 7
Copyright © 2021 HOCTAP247
