Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Bài tập theo tuần Toán 9 - Tuần 15 !!
Cho hai đường tròn (O) và (O') tiếp xúc ngoài...
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Đường thẳng qua A cắt (O)
Câu hỏi :
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Đường thẳng qua A cắt (O) tại B, cắt (O') tại
a) Chứng minh OB // O'C
b) Gọi d là tiếp tuyến tại B của đường tròn (O), d' là tiếp tuyến tại C của (O'). Chứng minh rằng d // d'.
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Đường thẳng qua A cắt (O) tại B, cắt (O') tại
a) Chứng minh OB // O'C
b) Gọi d là tiếp tuyến tại B của đường tròn (O), d' là tiếp tuyến tại C của (O'). Chứng minh rằng d // d'.
* Đáp án
* Hướng dẫn giải
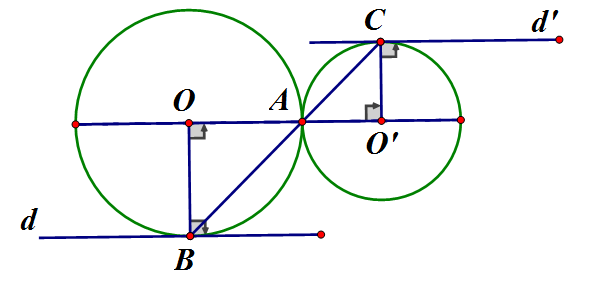
a) cân tại O
Mà (đối đỉnh), do đó:
(d là tiếp tuyến tại B của (O)) (d' là tiếp tuyến tại (C) của (O')). Do đó d // d'.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập theo tuần Toán 9 - Tuần 15 !!
Số câu hỏi: 8
Copyright © 2021 HOCTAP247
