Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Bài tập theo tuần Toán 9 - Tuần 17 !!
Vẽ tam giác ABC vuông tại A có AB =...
Vẽ tam giác ABC vuông tại A có AB = 4cm; AC = 5cm và AH là đường cao.
Câu hỏi :
Vẽ tam giác ABC vuông tại A có AB = 4cm; AC = 5cm và AH là đường cao.
a) Tính độ dài đoạn thẳng AH.
b) Tính các tỉ số lượng giác: tanB, sinC.
c) Gọi E là hình chiếu của H trên AB và F là hình chiếu của H trên AC.
Chứng minh AE.AB = AF.AC
Vẽ tam giác ABC vuông tại A có AB = 4cm; AC = 5cm và AH là đường cao.
a) Tính độ dài đoạn thẳng AH.
b) Tính các tỉ số lượng giác: tanB, sinC.
c) Gọi E là hình chiếu của H trên AB và F là hình chiếu của H trên AC.
Chứng minh AE.AB = AF.AC
* Đáp án
* Hướng dẫn giải
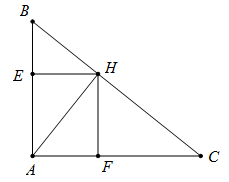
a) Có: hay
()
b) (= 1,25)
()
c) DAHB vuông tại H có HE là đường cao nên AE. AB = AH2
Tương tự có AF.AC = AH2 Þ AE. AB = AF.AC (cùng bằng AH2)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập theo tuần Toán 9 - Tuần 17 !!
Số câu hỏi: 16
Copyright © 2021 HOCTAP247
