Cho nửa đường tròn tâm O có đường kính AB. Gọi Ax, By là các tia vuông góc với AB

Câu hỏi :

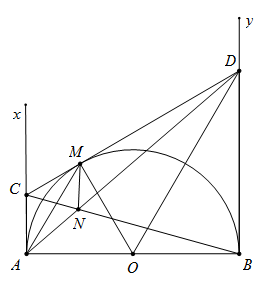
Cho nửa đường tròn tâm O có đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc nửa đường tròn (M khác A và B). Đường thẳng qua M vuông góc với OM cắt Ax tại C và cắt By tại D.

a) Chứng minh CA = CM.                                   

b) Chứng minh $\widehat{\text{MOB}}\text{ = 2.}\widehat{\text{ MAO}}$, từ đó suy ra AM song song với OD.     

c) Gọi N là giao điểm của AD và BC. Chứng minh đường thẳng MN vuông góc với đường thẳng AB.

* Đáp án

* Hướng dẫn giải

a) CM ^ MO Þ CM là tiếp tuyến của (O)

CA ^ AO Þ CA là tiếp tuyến của (O).

Þ CM = CA (T.chất 2 tt cắt nhau).

b) DOMA cân tại O do OM = OA

$\Rightarrow \widehat{\text{MAO}}=\widehat{\text{AMO}}$

Mà $\widehat{\text{MOB}}=\widehat{\text{MAO}}+\widehat{\text{AMO}}$ (góc ngoài)

$\Rightarrow \widehat{\text{MOB}}\text{ = 2 }\widehat{\text{MAO}}$

Lí luận được BD là tiếp tuyến của (O)

Þ OD là phân giác của $\widehat{\text{MOB}}$

Þ $\widehat{\text{MOB}}=\text{2 }\widehat{\text{DOB}}$ Þ$\widehat{\text{MAO}}=\widehat{\text{DOB}}$

Þ AM // OD

c) AC // BD Þ $\frac{\text{NC}}{\text{NB}}\text{=}\frac{\text{AC}}{\text{BD}}$

Mà AC = MC và BD = MD

Þ $\frac{\text{NC}}{\text{NB}}\text{=}\frac{\text{MC}}{\text{MD}}$Þ MN // BD Þ MN ^ AB