Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Bài tập theo tuần Toán 9 - Tuần 21 !!
Vẽ nửa đường tròn đường kính BC của tam giác...
Vẽ nửa đường tròn đường kính BC của tam giác đều ABC về phía ngoài
Câu hỏi :
Vẽ nửa đường tròn đường kính BC của tam giác đều ABC về phía ngoài của tam giác. Trên đường tròn đó lấy hai điểm D và E sao cho . Các tia AD, AE cắt cạnh BC tại M và N. Chứng minh rằng
Vẽ nửa đường tròn đường kính BC của tam giác đều ABC về phía ngoài của tam giác. Trên đường tròn đó lấy hai điểm D và E sao cho . Các tia AD, AE cắt cạnh BC tại M và N. Chứng minh rằng
* Đáp án
* Hướng dẫn giải
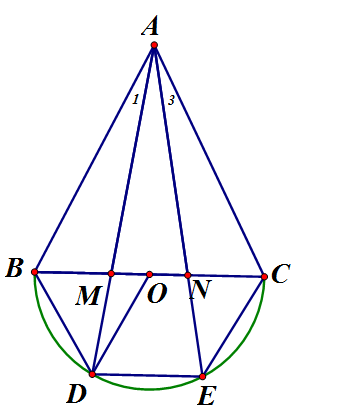
Xét và có: (góc nội tiếp chắn
Xét có đều
, mà hai góc ở vị trí so le trong nên , mà
Vì mà hai góc ở vị trí so le trong nên AB // OD
Áp dụng định lý Ta let ta có Chứng minh tương tự
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập theo tuần Toán 9 - Tuần 21 !!
Số câu hỏi: 27
Copyright © 2021 HOCTAP247
