Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Bài tập theo tuần Toán 9 - Tuần 22 !!
Tam giác đều ABC nội tiếp đường tròn (O). Vẽ...
Tam giác đều ABC nội tiếp đường tròn (O). Vẽ một đường tròn (O') tiếp xúc trong
Câu hỏi :
Tam giác đều ABC nội tiếp đường tròn (O). Vẽ một đường tròn (O') tiếp xúc trong với đường tròn (O) tại điểm T trên cung nhỏ AB và cắt các dây TA, TB, TC lần lượt tại D, E, F. Chứng minh rằng:
* Đáp án
* Hướng dẫn giải
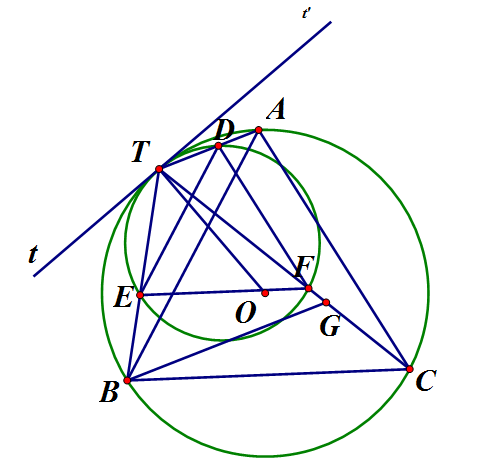
Qua T vẽ tiếp tuyến chung tTt'với hai đường tròn
Ta có: (tiếp tuyến – dây cung)
Tương tự:
Chứng minh tương tự :
Lấy G thuộc tia TC sao cho TG = TB
cân (TG = TB) và đều
Xét có: (cùng chắn
Do đó: mà (đpcm)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập theo tuần Toán 9 - Tuần 22 !!
Số câu hỏi: 18
Copyright © 2021 HOCTAP247
