Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Bài tập theo tuần Toán 9 - Tuần 23 !!
Trên đường tròn (O) lấy ba điểm A, B, C....
Trên đường tròn (O) lấy ba điểm A, B, C. Gọi M, N, P theo thứ tự là các điểm
Câu hỏi :
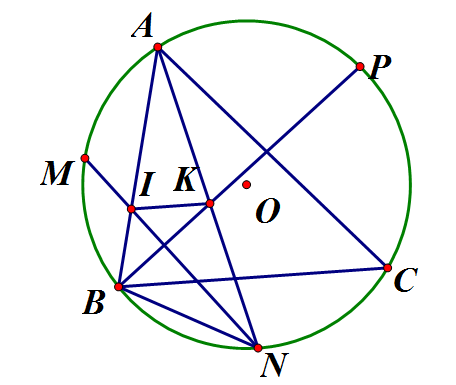
Trên đường tròn (O) lấy ba điểm A, B, C. Gọi M, N, P theo thứ tự là các điểm chính giữa của các cung AB, BC, AC. Gọi I là giao điểm của AB và MN, K là giao điểm của AN, BP. Chứng minh rằng:
cân
Trên đường tròn (O) lấy ba điểm A, B, C. Gọi M, N, P theo thứ tự là các điểm chính giữa của các cung AB, BC, AC. Gọi I là giao điểm của AB và MN, K là giao điểm của AN, BP. Chứng minh rằng:
cân
* Đáp án
* Hướng dẫn giải
Ta có: (góc nội tiếp cùng chắn
(góc có đỉnh bên trong đường tròn)
Mà PC = AP và
Dễ thấy (góc nội tiếp chắn hai cung bằng nhau) nên NI là phân giác
Ta có:
Theo chứng minh trên (câu a, b) , cân có NI là đường phân giác . Do đó IN cũng là đường trung trực của cạnh cân hay mà (góc nội tiếp chắn 2 cung bằng nhau)
Từ (1) và (2) suy ra
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập theo tuần Toán 9 - Tuần 23 !!
Số câu hỏi: 18
Copyright © 2021 HOCTAP247
