Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Bài tập theo tuần Toán 9 - Tuần 25 !!
Cho tam giác ABC vuông tại A. Đường tròn (O)...
Cho tam giác ABC vuông tại A. Đường tròn (O) đường kính AB cắt BC tại M.
Câu hỏi :
Cho tam giác ABC vuông tại A. Đường tròn (O) đường kính AB cắt BC tại M.
a) Chứng minh và
b) Gọi I là trung điểm của AC. Đường thẳng BI cắt đường tròn (O) tại điểm thứ hai là N. Chứng minh MNCI là tứ giác nội tiếp
Chứng minh
Cho tam giác ABC vuông tại A. Đường tròn (O) đường kính AB cắt BC tại M.
a) Chứng minh và
b) Gọi I là trung điểm của AC. Đường thẳng BI cắt đường tròn (O) tại điểm thứ hai là N. Chứng minh MNCI là tứ giác nội tiếp
Chứng minh
* Đáp án
* Hướng dẫn giải
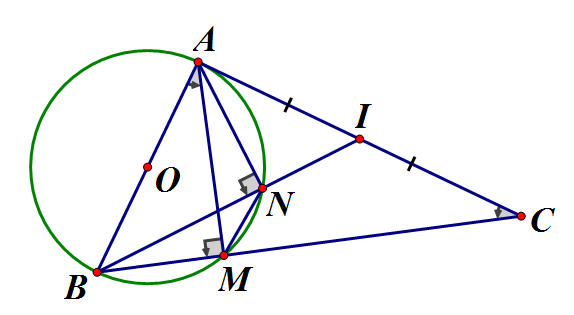
Ta có: (góc nội tiếp chắn nửa đường tròn)
Ta có vuông tại A, AM là đường cao (hệ thức lượng)
Ta có (cùng chắn cung BM)
Mà (cùng phụ )
là tứ giác nội tiếp
Ta có: (góc nội tiếp chắn nửa đường tròn)
Xét và có: chung
Mà AI = IC (gt)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập theo tuần Toán 9 - Tuần 25 !!
Số câu hỏi: 15
Copyright © 2021 HOCTAP247
