Cho nửa đường tròn (O) đường kính BC = 2a. A là điểm trên nửa đường tròn,

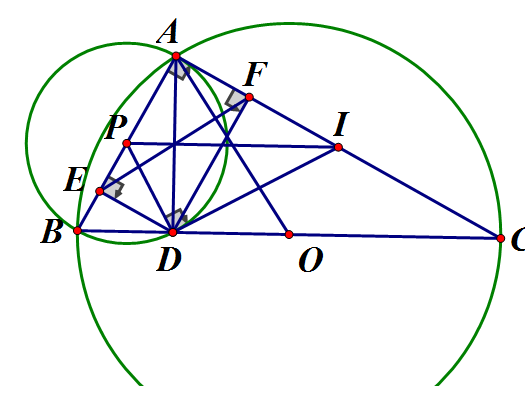
a) Ta có: $\widehat{AOB}=2\widehat{ACB}$(góc nội tiếp và góc ở tâm cùng chắn cung AB)

$\Rightarrow \widehat{AOB}=2\alpha$

b) Ta có $\widehat{BAC}={90}^0$ (góc nội tiếp chắn nửa đường tròn)

Chứng minh tương tự $\Rightarrow \widehat{ADB}={90}^0$

Ta có: $\widehat{A}=\widehat{E}=\widehat{F}={90}^0\Rightarrow AED\text{}F$ là hình chữ nhật $\Rightarrow \widehat{EAD}=\widehat{AEF}$

Mà $\widehat{EAD}=\widehat{ACB}$ (cùng phụ $\widehat{ABD})\Rightarrow \widehat{AEF}=\widehat{ACB}$

$\Rightarrow BE\text{}FC$ là tứ giác nội tiếp

c) $S_{quat\stackrel{⏜}{AB}}=\frac{\pi R^2.2\alpha }{{360}^0}=\frac{\pi R^2\alpha }{{180}^0}\left(dvdt\right)$

$\Delta ADO$ vuông tại D $\Rightarrow \sin O=\frac{AD}{AO}\Rightarrow AD=R.\sin 2\alpha$

$\iff S_{AOB}=\frac{1}{2}OB.AD=\frac{1}{2}R.R\sin 2\alpha =\frac{R^2\sin 2\alpha }{2}$

d) Gọi P là tâm đường tròn đường kính AB

Xét $\Delta PAI$ và $\Delta PDI$ có: $\widehat{PAI}=\widehat{PDI}={90}^0,PA=PD,PI$ chung

$\Rightarrow \Delta PAI=\Delta PDI(ch-cgv)\Rightarrow DI=AI\left(1\right)$

$\Delta ADC$ vuông tại D $\left(do\widehat{ADB}={90}^0-cmt\right)$ mà $AI=DI\Rightarrow \Delta ADI$ cân tại I.

$\Rightarrow \widehat{DAI}=\widehat{ADI}\Rightarrow {90}^0-\widehat{DAI}={90}^0-\widehat{ADI}\Rightarrow \widehat{IDC}=\widehat{ICD}$$\Rightarrow \Delta DIC$ cân tại I$\Rightarrow DI=IC\left(2\right)$

Từ (1) và (2) $\Rightarrow AI=IC\Rightarrow DI$ là đường trung tuyến $\Delta ADC$

Khi DI // EF $\Rightarrow \widehat{EFD}=\widehat{FDI}$(So le trong)

Mà ta có $\widehat{ADF}=\widehat{DAB}=\widehat{ICD}=\widehat{IDC}=\alpha$

Mà $\widehat{EFD}=\widehat{DAB}$ (Tính chất hình chữ nhật)

$\Rightarrow \widehat{ADF}=\widehat{FDI}=\widehat{IDC}=\alpha$ mà $\widehat{ADF}+\widehat{FDI}+\widehat{IDC}=\widehat{ADC}={90}^0$

$\Rightarrow 3\alpha ={90}^0\Rightarrow \alpha ={30}^0$