Cho đường tròn (O; R) đường kính AB cố định. Gọi M là trung điểm đoạn OB

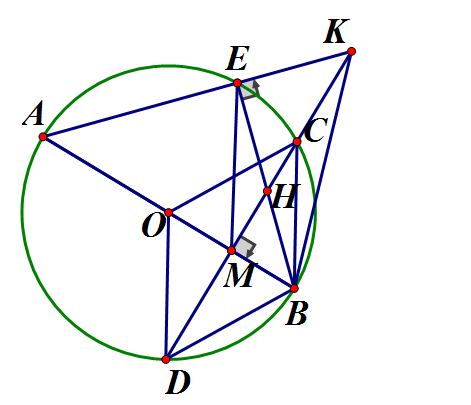
a) Ta có $\angle AEB={90}^0$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow \angle KEB=\angle KMB={90}^0\Rightarrow$ Tứ giác BMEK có đỉnh M, E liên tiếp cùng nhìn BK dưới 1 góc vuông nên BMEK là tứ giác nội tiếp

$\Rightarrow B,M,E,K$ cùng thuộc một đường tròn

b) Ta có $AM\perp CD$ tại trung điểm M của CD (tính chất đường kính – dây cung)

$\Rightarrow CODB$ có hai đường chéo vuông góc tại trung điểm mỗi đường$\Rightarrow CODB$ là hình thoi

$\Rightarrow OC=CB=OB=R\Rightarrow COB$ đều