Cho tam giác ABC có góc BAC = 45 độ. Các góc B, C đều nhọn. Đường tròn đường

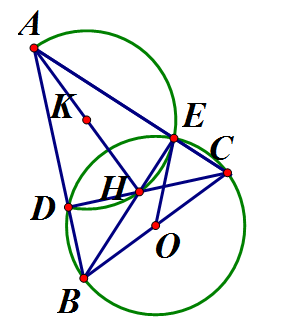
a) Chứng minh: AE = BE

Ta có : $\angle BEA={90}^0$ (góc nội tiếp chắn nửa đường tròn)$\Rightarrow \angle AEB={90}^0$

$\Delta AEB$ vuông ở E có $\angle BAE={45}^0$ nên vuông cân $\Rightarrow AE=BE$

b) $\angle BDC={90}^0\Rightarrow \angle ADH={90}^0$

Tứ giác ADHE có $\angle ADH+\angle AEH={180}^0$ nên nội tiếp đường tròn, tâm K của đường tròn này là trung điểm AH

c) $\Delta AEH$ vuông ở E có K là trung điểm AH nên $KE=KA=\frac{1}{2}AH$

Vậy $\Delta AKE$ cân ở K. Do đó $\angle KAE=\angle KEA$

$\Delta EOC$ cân ở O (do $OC=OE)\Rightarrow \angle OCE=\angle OEC\Rightarrow H$ là trực tâm $\Delta ABC\Rightarrow AH\perp BC$

$\angle HAC+\angle ACO={90}^0\Rightarrow \angle AEK+\angle OEC={90}^0$

Do đó $\angle KEO={90}^0\Rightarrow OE\perp KE$

Điểm K là tâm đường tròn ngoại tiếp tứ giác ADHE nên cũng là tâm đường tròn ngoại tiếp $\Delta ADE$

Vậy OE là tiếp tuyến đường tròn ngoại tiếp $\Delta ADE$

d) Ta có : $\angle DOE=2\angle ABE={2.45}^0={90}^0$ (cùng chắn cung DE)

$\Rightarrow S_{quat\left(DOE\right)}=\frac{\pi a^2{.90}^0}{{360}^0}=\frac{\pi a^2}{4}$;   $S_{DOE}=\frac{1}{2}OD.OE=\frac{1}{2}{a}^2$

Vậy diện tích viên phân cung DE là :