Cho ∆ABC nhọn (AB < AC) nội tiếp đường tròn (O) và 2 đường cao BD, CE cắt nhau tại H (D AC, E AB). a) Chứng minh tứ giác BEDC nội tiếp. b) Vẽ đường kính AM của đường tròn (O),...
Câu hỏi :
Cho ∆ABC nhọn (AB < AC) nội tiếp đường tròn (O) và 2 đường cao BD, CE cắt nhau tại H (D Î AC, E Î AB).
a) Chứng minh tứ giác BEDC nội tiếp.
b) Vẽ đường kính AM của đường tròn (O), AH cắt BC tại F (F Î BC).
Chứng minh: AB.AC = AF.AM
c) Tia DE và CB cắt nhau tại K. AK cắt đường tròn (O) tại N. Chứng minh: N, H, M thẳng hàng.
Cho ∆ABC nhọn (AB < AC) nội tiếp đường tròn (O) và 2 đường cao BD, CE cắt nhau tại H (D Î AC, E Î AB).
a) Chứng minh tứ giác BEDC nội tiếp.
b) Vẽ đường kính AM của đường tròn (O), AH cắt BC tại F (F Î BC).
Chứng minh: AB.AC = AF.AM
c) Tia DE và CB cắt nhau tại K. AK cắt đường tròn (O) tại N. Chứng minh: N, H, M thẳng hàng.
* Đáp án
* Hướng dẫn giải
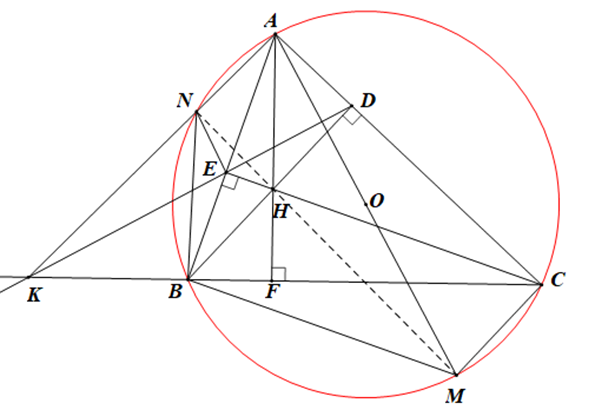
a) Ta có: = 90° (CE ^ AB), = 90° (BD ^ AC)
Þ = 90°
Mà và là hai góc có đỉnh kề nhau cùng nhìn cạnh BC của tứ giác BEDC.
Þ Tứ giác BEDC nội tiếp.
b) Ta có điểm C nằm trên đường tròn (O) đường kính AM
Nên = 90° (góc nội tiếp chắn nửa đường tròn)
Mà AH cắt BC tại F nên AF ⊥ BC do đó
Suy ra = 90°
Xét ∆ACM và ∆ABF, có:
= 90° (chứng minh trên),
(hai góc nội tiếp cùng chắn cung AC của (O))
Þ ∆ACM ᔕ ∆AFB (g.g)
Þ (tỉ số đồng dạng)
Þ AB.AC = AF.AM (đpcm).
c) • Tứ giác BEDC là tứ giác nội tiếp (chứng minh câu a)
Þ (hai góc nội tiếp cùng chắn cung EB)
Hay
Xét DKDB và DKCE có:
(Chứng minh trên),
là góc chung
Þ DKDB ᔕ DKCE (g.g)
(tỉ số đồng dạng)
Þ KB.KC = KD.KE (1)
• Tứ giác ANBC nội tiếp
Xét DKBN và DKAC có:
là góc chung,
(chứng minh trên)
Þ DKBN ᔕ DKAC (g.g)
(tỉ số đồng dạng)
Þ KB. KC = KA.KN (2)
Từ (1) và (2) ta có:
KD.KE = KA.KN (= KB. KC)
Xét DKNE và DKAD có:
là góc chung,
(chứng minh trên)
Þ DKNE ᔕ DKAD (c.g.c)
(hai góc tương ứng)
Þ Tứ giác ANED nội tiếp đường tròn.
Do đó 4 điểm A, N, E, D cùng thuộc một đường tròn (3)
• Tứ giác AEHD có
Þ E và D cùng thuộc đường tròn đường kính AH
Þ 4 điểm A, E, H, D cùng thuộc đường tròn đường kính AH (4)
Từ (3) và (4) suy ra 5 điểm A, N, E, H, D cùng thuộc đường tròn đường kính AH
Do đó tứ giác ANHD nội tiếp đường tròn
(góc nội tiếp chắn nửa đường tròn)
Þ AN ⊥ HN tại N (5)
• Ta có điểm N nằm trên đường tròn đường kính AM
= 90° (góc nội tiếp chắn nửa đường tròn)
Þ AN ⊥ MN tại N (6)
Từ (5) và (6) ta có: MN ≡ HN
Do đó ba điểm N, H, M thẳng hàng.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án !!
Copyright © 2021 HOCTAP247
