Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Bài tập theo tuần Toán 9 - Tuần 35 !!
Cho hình vuông ABCD có cạnh bằng a. Trên cạnh...
Cho hình vuông ABCD có cạnh bằng a. Trên cạnh AB lấy điểm E tùy ý sao cho AE = x
Câu hỏi :
Cho hình vuông ABCD có cạnh bằng a. Trên cạnh AB lấy điểm E tùy ý sao cho AE = x với 0 < x < a. Qua A kẻ đường thẳng d vuông góc với CE, đường thẳng d cắt hai đường thẳng CE và CB lần lượt tại M và N
a) Chứng minh MNBE là tứ giác nội tiếp
b) Tính số đo
c) Tính diện tích hình tròn ngoại tiếp tứ giác MNBE theo a và x
Cho hình vuông ABCD có cạnh bằng a. Trên cạnh AB lấy điểm E tùy ý sao cho AE = x với 0 < x < a. Qua A kẻ đường thẳng d vuông góc với CE, đường thẳng d cắt hai đường thẳng CE và CB lần lượt tại M và N
a) Chứng minh MNBE là tứ giác nội tiếp
b) Tính số đo
c) Tính diện tích hình tròn ngoại tiếp tứ giác MNBE theo a và x
* Đáp án
* Hướng dẫn giải
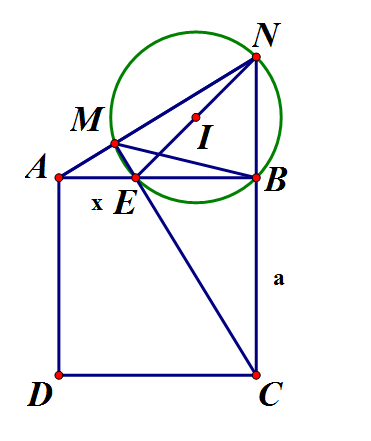
a) là tứ giác nội tiếp
b) Xét và có (cùng phụ )
vuông cân tại B
Mà (cùng nhìn cạnh BN)
c) Vì suy ra tâm đường tròn ngoại tiếp MNBE là trung điểm I của EN
vuông cân tại B
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập theo tuần Toán 9 - Tuần 35 !!
Số câu hỏi: 14
Copyright © 2021 HOCTAP247
