(3,0 điểm) Cho đường tròn tâm O, bán kính R và điểm A ở ngoài đường tròn (O; R) sao cho AO > 2R. Kẻ 2 tiếp tuyến AB, AC (B, C là các tiếp điểm). Gọi H là giao điểm của AO và BC. a)...
Câu hỏi :
(3,0 điểm) Cho đường tròn tâm O, bán kính R và điểm A ở ngoài đường tròn (O; R) sao cho AO > 2R. Kẻ 2 tiếp tuyến AB, AC (B, C là các tiếp điểm). Gọi H là giao điểm của AO và BC.
a) Chứng minh tứ giác ABOC nội tiếp và OH.OA = R2.
b) Kẻ dây cung BD của đường tròn (O; R) song song với AO. Đoạn AD cắt (O; R) tại E (khác D). Gọi F là trung điểm của DE. Chứng minh tứ giác ABFO nội tiếp và tam giác BEF vuông.
c) Kẻ đường kính BK của đường tròn (O; R). Chứng minh tia AO là phân giác của góc DAK.
(3,0 điểm) Cho đường tròn tâm O, bán kính R và điểm A ở ngoài đường tròn (O; R) sao cho AO > 2R. Kẻ 2 tiếp tuyến AB, AC (B, C là các tiếp điểm). Gọi H là giao điểm của AO và BC.
a) Chứng minh tứ giác ABOC nội tiếp và OH.OA = R2.
b) Kẻ dây cung BD của đường tròn (O; R) song song với AO. Đoạn AD cắt (O; R) tại E (khác D). Gọi F là trung điểm của DE. Chứng minh tứ giác ABFO nội tiếp và tam giác BEF vuông.
c) Kẻ đường kính BK của đường tròn (O; R). Chứng minh tia AO là phân giác của góc DAK.
* Đáp án
* Hướng dẫn giải
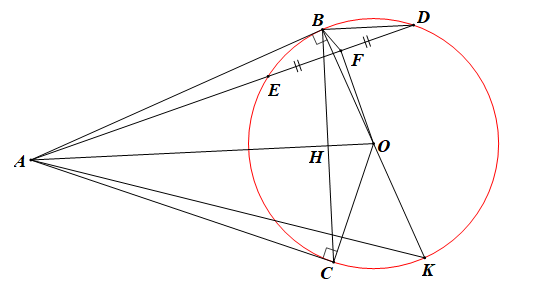
a) Ta có: AB, AC là 2 tiếp tuyến
Þ AB ^ OB; AC ^ OC
Xét tứ giác ABOC có
Þ Hai điểm B và C cùng nằm trên đường tròn đường kính AO
Þ Tứ giác ABOC nội tiếp đường tròn đường kính AO.
Vì AB, AC là hai tiếp tuyến của (O) cắt nhau tại A
Nên AB = AC và OB = OC (tính chất hai tiếp tuyến cắt nhau)
Suy ra A và O cùng nằm trên đường trung trực của BC
Do đó AO là đường trung trực của BC.
Þ AO ⊥ BC.
Xét ∆ABO vuông tại B ( ), BH ^ AO (BC ^ AO, H Î BC)
Theo hệ thức lượng trong tam giác vuông ta có:
OB2 = OH.OA
Þ OH.OA = R2.
b) F là trung điểm ED
Þ OF ^ ED (liên hệ giữa dây cung và đường kính)
Xét tứ giác ABFO có
Mà và là hai góc có đỉnh kề nhau của tứ giác ABFO
Þ Tứ giác ABFO nội tiếp
Þ (hai góc nội tiếp cùng chắn cung AB)
Mà (2 góc cùng chắn cung BD) và (Tam giác OBC cân tại O).
=>
Mà (do ∆BHO vuông tại H).
Þ
Þ Tam giác BEF vuông tại B.
c) Xét ∆ABO và ∆ACO có :
AO chung,
OB = OC = R,
Þ ∆ABO = ∆ACO (cạnh huyền – cạnh góc vuông)
Þ (hai góc tương ứng)
Mà BD // AO Þ BD ^ BC
Þ
Þ CD là đường kính của (O)
Xét ∆BDC và ∆CBK có:
CD = BK = 2R,
,
BC chung,
Þ ∆BDC = ∆CBK (cạnh huyền – cạnh góc vuông)
Þ BD = CK
Ta có:
Mà (hai góc nội tiếp cùng chắn cung DK)
Xét ∆ABD và ∆ACK có:
AB = AC (chứng minh câu a),
(chứng minh trên),
BD = CK
Þ ∆ABD = ∆ACK (c.g.c)
Þ (hai góc tương ứng)
Tam giác ABC có AB = AC (chứng minh trên)
Nên DABC cân tại A
(tính chất tam giác cân)
=>
Þ AO là phân giác góc DAK.
Vậy AO là phân giác góc DAK.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án !!
Copyright © 2021 HOCTAP247
