Cho tam giác nhọn ABC nội tiếp đường tròn (O), các đường cao BD và CE của tam giác ABC cắt nhau tại H. 1) Tính BDC
Câu hỏi :
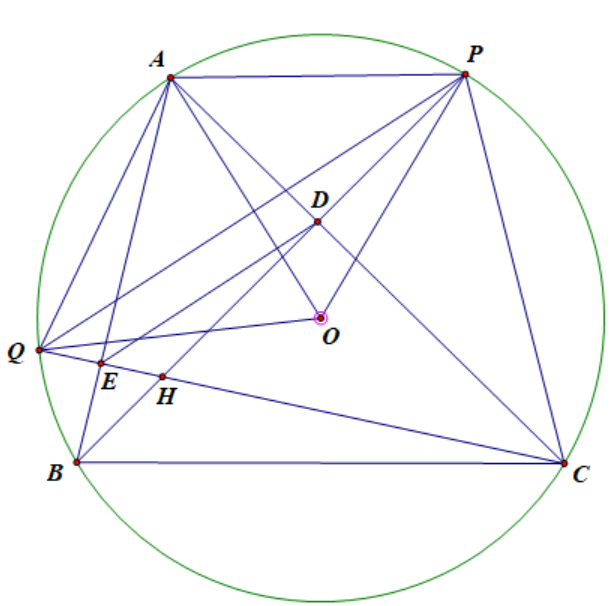
Cho tam giác nhọn ABC nội tiếp đường tròn (O), các đường cao BD và CE của tam giác ABC cắt nhau tại H.
1) Tính .
2) Chứng minh AEHD là tứ giác nội tiếp.
3) Các đường thẳng BD và CE cắt đường tròn (O) theo thứ tự tại P và Q (P khác B, Q khác C). Chứng minh HB.HP = HC.HQ.
4) Chứng minh OA vuông góc DE.
Cho tam giác nhọn ABC nội tiếp đường tròn (O), các đường cao BD và CE của tam giác ABC cắt nhau tại H.
1) Tính .
2) Chứng minh AEHD là tứ giác nội tiếp.
3) Các đường thẳng BD và CE cắt đường tròn (O) theo thứ tự tại P và Q (P khác B, Q khác C). Chứng minh HB.HP = HC.HQ.
4) Chứng minh OA vuông góc DE.
* Đáp án
* Hướng dẫn giải
a) Ta có BD ^ AC (gt) Þ = 90°
b) Ta có
CE ^ AB (gt) Þ = 90°
BD ^ AC (gt) Þ = 90°
Þ = 180°
Þ AEHD là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng 180°).
3) Xét ∆BHQ và ∆CHP có:
(Hai góc đổi đỉnh)
(Hai góc nội tiếp cùng chắn cung BC của đường tròn (O)).
Nên ∆BHQ ∆CHP (g.g)
Þ Þ HB.HP = HC.HQ
4) Ta có
= 90° (chứng minh trên)
Mà hai góc và cùng nhìn đoạn thẳng BC dưới một góc vuông
Vậy tứ giác BCDE nội tiếp đường tròn đường kính BC.
Þ (góc nội tiếp cùng chắn cung BE của đường tròn ngoại tiếp tứ giác BCDE) (1).
Có (góc nội tiếp cùng chắn cung BQ của đường tròn (O)) (2).
Từ (1) và (2) Þ
Mà hai góc này ở vị trí đồng vị Þ PQ // DE (*).
Ta có (góc nội tiếp cùng chắn cung DE của đường tròn nội tiếp tứ giác BCDE).
Hay Û AP = AQ (3).
Mặt khác: OP = OQ (cùng là bán kính của đường tròn (O)) (4).
Từ (3) và (4) Þ OA là đường trung trực của đoạn thẳng PQ Þ OA ^ PQ (*)(*).
Từ (*) và (*)(*) suy ra OA ^ DE (đpcm).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án !!
Copyright © 2021 HOCTAP247
