Cho đường tròn (O) và điểm E nằm ngoài đường tròn. Vẽ cát tuyến EAB và ECD với đường tròn (A nằm giữa E và B, C nằm giữa E và D)

* Hướng dẫn giải

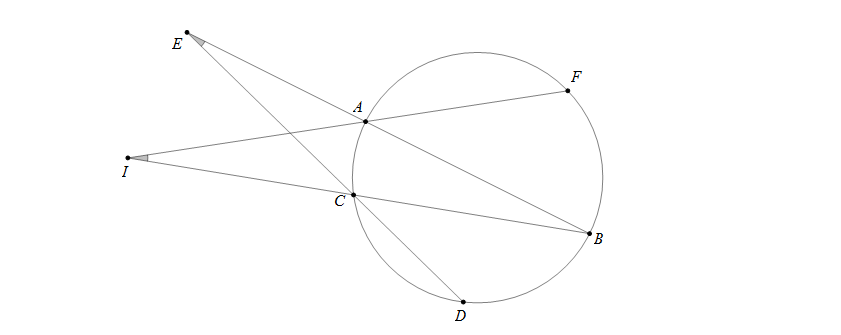
B nằm chính giữa DF nên sđ\(\stackrel\frown{BD}=\)sđ\(\stackrel\frown{BF}\)

Mặt khác góc tại E và I là hai góc có đỉnh nằm bên ngoài đường tròn nên \(\widehat{E}=\frac{1}{2}\)(sđ\(\stackrel\frown{BD}-\) sđ\(\stackrel\frown{AC}\))\(=\frac{1}{2}\)(sđ\(\stackrel\frown{BF}-\) sđ\(\stackrel\frown{AC}\))\(=\widehat{I}\).

Theo đề bài ta có \(\widehat{I}=\widehat{E}=25^0\).