Cho điểm A ở bên ngoài đường tròn (O), kẻ cát tuyến ABC với đường tròn và hai tiếp tuyến AE,AF đến đường tròn. Gọi H là giao điểm của AO và EF
Câu hỏi :
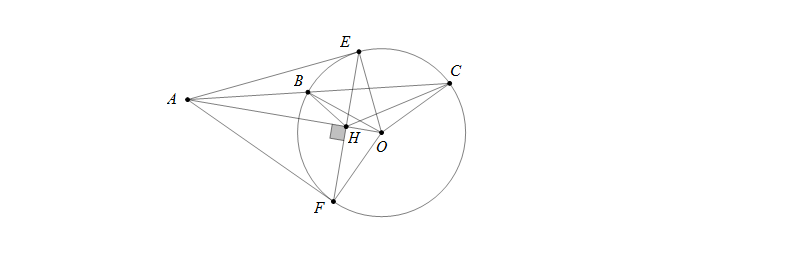
Cho điểm A ở bên ngoài đường tròn (O), kẻ cát tuyến ABC với đường tròn và hai tiếp tuyến AE,AF đến đường tròn. Gọi H là giao điểm của AO và EF. Khẳng định nào sau đây là sai:
A. \(AO\perp EF\)
B. HE là tia phân giác của \(\widehat{BHC}\)
C. \(AB.AC=AO^2\)
D. Tứ giác BHOC nội tiếp.
* Đáp án
C
* Hướng dẫn giải
+ \(AH\perp EF\) (tính chất quen thuộc)
+ Ta đã biết \(AE^2=AB.AC\) (xem lại ở phần bài tập nâng cao)
Mặt khác, áp dụng hệ thức lượng cho tam giác vuông AEO với đường cao EH, ta có \(AE^2=AH.AO\)
Do đó \(AB.AC=AH.AO\Rightarrow \frac{AB}{AH}=\frac{AO}{AC}\)
Xét \(\bigtriangleup ABH\) và \(\bigtriangleup AOC\) có \(\widehat{OAC}\) chung và \(\frac{AB}{AH}=\frac{AO}{AC}\) nên \(\bigtriangleup ABH \sim \bigtriangleup AOC\)
Suy ra \(\widehat{AHB}=\widehat{ACO}\) \(\Rightarrow\) Tứ giác BHOC nội tiếp (câu D đúng)
+ Ta có \(\widehat{CHO}=\widehat{CBO}=\widehat{BCO}=\widehat{BHA}\) từ đó suy ra \(\widehat{EHC}=\widehat{EHB}(=90^0-\widehat{CHO})\)
nên HE là phân giác của góc BHC (câu B đúng)
+ Câu C sai vì \(AB.AC=AH.AO\neq AO^2\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Hình học 9 Bài 7 Tứ giác nội tiếp
Copyright © 2021 HOCTAP247
