Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Trắc nghiệm Hình học 9 Bài 1 Sự xác định của đường tròn Tính chất đối xứng của đường tròn
Cho tam giác ABC nhọn. Đường tròn đường kính BC...
Cho tam giác ABC nhọn. Đường tròn đường kính BC cắt AB tại N, AC tại M. Gọi H là giao điểm của CN và BM. Khi đó A,N,H,M cùng nằm trên đường tròn nào?
Câu hỏi :
Cho tam giác ABC nhọn. Đường tròn đường kính BC cắt AB tại N, AC tại M. Gọi H là giao điểm của CN và BM. Khi đó A,N,H,M cùng nằm trên đường tròn nào?
A. \((I;IM)\), I là trung điểm MN
B. \((I;IH)\), I là trung điểm MN
C. \((F;FA)\), F là giao điểm đường tròn với AH
D. \((E;EA)\), E là trung điểm AH
* Đáp án
D
* Hướng dẫn giải
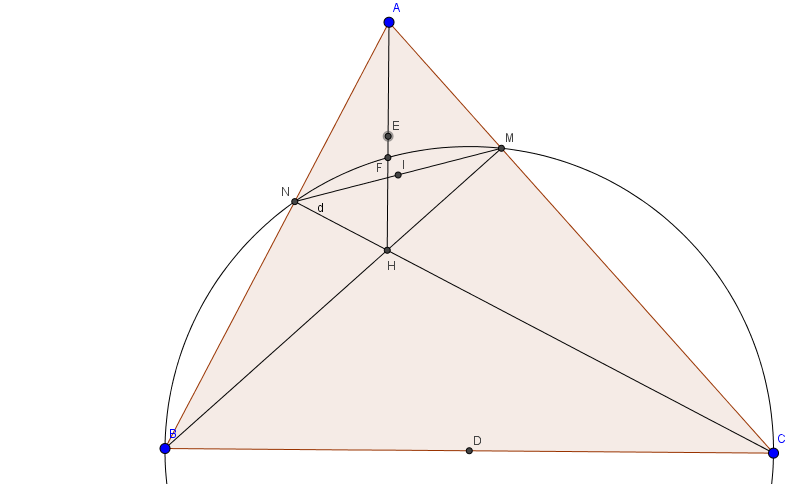
Trước tiên: hai tam giác BNC và BMC là hai tam giác lần lượt vuông tại N và M. Đường tròn đường kính BC đi qua M,N
Xét hai tam giác ANH và AMH cũng lần lượt vuông tại N,M. Với E là trung điểm AH, Ah là cnahj huyền của cả hai tam giác
nên đường tròn tâm E bán kính EA sẽ đi qua M, N, H.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Hình học 9 Bài 1 Sự xác định của đường tròn Tính chất đối xứng của đường tròn
Số câu hỏi: 5
Copyright © 2021 HOCTAP247
