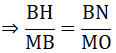Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Đề thi Học kì 1 Toán 9 chọn lọc, có đáp án !!
Kẻ đường kính AN của đường tròn (O). Kẻ BH...
Kẻ đường kính AN của đường tròn (O). Kẻ BH vuông góc với AN tại H
Câu hỏi :
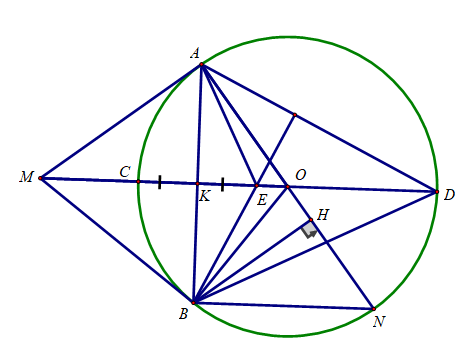
Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
* Đáp án
* Hướng dẫn giải
c) Ta có: ∠(ABN ) = (B thuộc đường tròn đường kính AN)
⇒ BN // MO ( cùng vuông góc với AB)
Do đó:
∠(AOM) = ∠(ANB) (đồng vị))
∠(AOM) = ∠(BOM) (OM là phân giác ∠(AOB))
⇒ ∠(ANB) = ∠(BOM)
Xét ΔBHN và ΔMBO có:
∠(BHN) = ∠(MBO ) =
∠(ANB) = ∠(BOM)
⇒ ΔBHN ∼ ΔMBO (g.g)
Hay MB. BN = BH. MO
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi Học kì 1 Toán 9 chọn lọc, có đáp án !!
Số câu hỏi: 74
Copyright © 2021 HOCTAP247