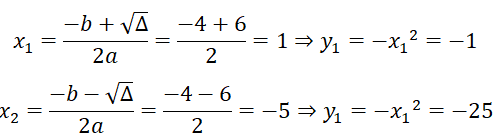Cho hàm số y= - x^2 (P) và đường thẳng (d): y=2mx-5 Chứng tỏ rằng trên mặt

* Hướng dẫn giải

b) Phương trình hoành độ giao điểm của (P) và (d) là:

-$x^2$ = 2mx - 5 ⇔ $x^2$ + 2mx - 5 = 0

Δ'= $m^2$+ 5 > 0 với ∀m ∈ R

Vậy trên mặt phẳng Oxy đường thẳng (d) và Parabol (P) luôn cắt nhau tại hai điểm phân biệt.

Khi m = 2, phương trình hoành độ giao điểm của (P) và (d) là:

-$x^2$= 4x - 5 ⇔ $x^2$ + 4x - 5 = 0

Δ =$4^2$ - 4.1.(-5) = 36

⇒ Phương trình có 2 nghiệm

Vậy tọa độ hai giao điểm là M(1;-1) và N(-5;-25)