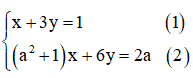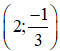Giải hệ phương trình x+3y=1 và (a^2+1)x+6y=2a trong mỗi trường hợp sau: a) a = -1;
Câu hỏi :
Giải hệ phương trình trong mỗi trường hợp sau:
* Đáp án
* Hướng dẫn giải
Cách 1
Ta có:
Từ (1) rút ra được x = 1 – 3y (*)
Thay vào phương trình (2) ta được :
a) a = -1, phương trình (**) trở thành : 0y = 4
Phương trình trên vô nghiệm
Vậy hệ phương trình khi a = -1 vô nghiệm.
b) a = 0, phương trình (**) trở thành -3y = 1 ⇔
Thay 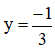
Vậy hệ phương trình khi a = 0 có nghiệm duy nhất
c) a = 1, phương trình (**) trở thành: 0y = 0
Phương trình nghiệm đúng với mọi y.
Vậy hệ phương trình khi a = 1 có vô số nghiệm dạng (1 – 3y; y) (y ∈ R).
Cách 2
a) Thay a = -1 vào hệ phương trình ta được hệ phương trình mới:
Vậy hệ phương trình vô nghiệm khi a= - 1.
b) Thay a = 0 vào hệ phương trình ta được hệ phương trình mới:
c) Thay a=1 vào hệ phương trình ta được hệ phương trình mới:
Vậy với a= 1 hệ phương trình có vô số nghiệm với nghiệm tổng quát là (-3y+1;y),(y ∈ R)
Kiến thức áp dụng
+ Giải hệ phương trình 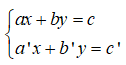
Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
+ Nếu xuất hiện phương trình dạng 0x = a (hoặc 0y = a) thì ta kết luận hệ phương trình vô nghiệm nếu a ≠ 0 hoặc hệ có vô số nghiệm nếu a = 0.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải bài tập SGK Toán 9 tập 2 hay nhất Luyện tập trang 15-16 !!
Copyright © 2021 HOCTAP247