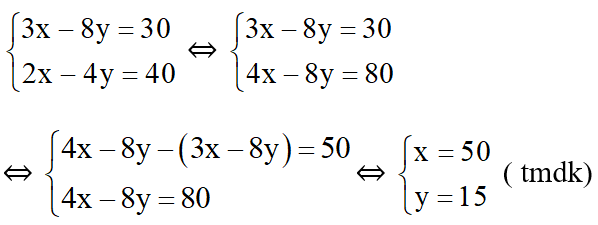Nhà Lan có một mảnh vườn trồng rau cải bắp. Vườn được đánh thành
Câu hỏi :
Nhà Lan có một mảnh vườn trồng rau cải bắp. Vườn được đánh thành nhiều luống, mỗi luống trồng cùng một số cây cải bắp. Lan tính rằng: Nếu tăng thêm 8 luống rau, nhưng mỗi luống trồng ít đi 3 cây thì số cây toàn vườn ít đi 54 cây. Nếu giảm đi 4 luống, nhưng mỗi luống trồng tăng thêm 2 cây thì số rau toàn vườn sẽ tăng thêm 32 cây. Hỏi vườn nhà Lan trồng bao nhiêu cây rau cải bắp?
* Đáp án
* Hướng dẫn giải
Gọi x là số luống rau, y là số cây mỗi luống.
Điều kiện x > 4, y > 3; x,y ∈ N
Số cây trong vườn là: x.y (cây)
+ Tăng 8 luống, mỗi luống ít hơn 3 cây thì số luống là x + 8, số cây mỗi luống là y – 3
⇒ Tổng số cây trong vườn là (x + 8)(y – 3) cây.
Số cây trong vườn ít đi 54 cây nên ta có phương trình:
(x + 8)(y – 3) = xy – 54
⇔ xy -3x + 8y - 24 = xy – 54
⇔ xy -3x + 8y - xy = –54 + 24
⇔ -3x + 8y = –30
⇔ 3x – 8y = 30
+ Giảm 4 luống mỗi luống tăng thêm 2 cây thì số luống là x – 4 và số cây mỗi luống là y + 2.
⇒ Số cây trong vườn là: (x – 4)(y + 2) cây
Số cây trong vườn tăng thêm 32 cây nên ta có phương trình:
(x – 4)(y + 2) = xy + 32
⇔ xy – 4y + 2x – 8 = xy + 32
⇔ 2x – 4y = 40
Ta có hệ phương trình:
Vậy số rau cải bắp nhà Lan trồng là : 15.50 = 750 cây.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình:
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải bài tập SGK Toán 9 tập 2 hay nhất Luyện tập (trang 24-25 sgk) !!
Copyright © 2021 HOCTAP247