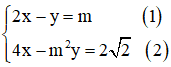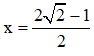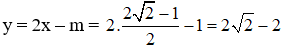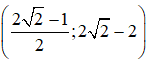Giải hệ phương trình 2x-y = m và 4x - m^2 y = 2 căn 2 trong mỗi trường hợp sau:

* Hướng dẫn giải

Xét (I): 

Từ phương trình (1) ta rút ra được y = 2x – m (*)

Thay (*) vào phương trình (2) ta được:

    4x – m2.(2x – m) = 2√2

    ⇔ 4x – 2m2.x + m3 = 2√2

    ⇔ (4 – 2m2).x = 2√2 – m3 (**)

a) Với m = -√2, phương trình (**) trở thành: 0x = 4√2

Phương trình vô nghiệm.

Vậy với m = -√2, hệ phương trình (I) vô nghiệm.

b) Với m = √2, phương trình (**) trở thành: 0x = 0

Phương trình nghiệm đúng với mọi x ∈ R, khi đó y = 2x – √2

Vậy với m = √2, hệ (I) có vô số nghiệm dạng (x ; 2x - √2), x ∈ R

c) Với m = 1, phương trình (**) trở thành: 2x = 2√2 – 1 ⇔ 

Thay vào (*) ta được:

Vậy hệ phương trình có nghiệm duy nhất