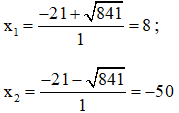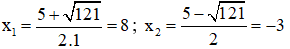Tìm hai số u và v trong mỗi trường hợp sau: a) u + v = 42, uv = 441

* Hướng dẫn giải

a) S = 42; P = 441 $\Rightarrow S^2 – 4P = {42}^2 – 4.441 = 0$

⇒ u và v là hai nghiệm của phương trình: $x^2 – 42x + 441 = 0$

Có:$\Delta ’ = {(-21)}^2 – 441 = 0$

⇒ Phương trình có nghiệm kép $x_1 = x_2 = -b’/a = 21.$

Vậy u = v = 21.

b) S = -42; P = -400 $\Rightarrow S2 – 4P = {(-42)}^2 – 4.(-400) = 3364 > 0$

⇒ u và v là hai nghiệm của phương trình: $x^2 + 42x – 400 = 0$

Có $\Delta ’ = {21}^2 – 1.(-400) = 841$

⇒ Phương trình có hai nghiệm phân biệt:

Vậy u = 8; v = -50 hoặc u = -50; v = 8.

c) u – v = 5 ⇒ u + (-v) = 5

u.v = 24 ⇒ u.(-v) = -uv = -24.

Ta tìm u và –v. Từ đó, ta dễ dàng tính được u và v.

S= u + (-v) = 5; P = u. (-v) = -24 ⇒ $S^2 – 4P = 5^2 – 4.(-24) = 121 > 0$

⇒ u và –v là hai nghiệm của phương trình: $x^2 – 5x – 24 = 0$

Có $\Delta = {(-5)}^2 – 4.1.(-24) = 121$

⇒ Phương trình có hai nghiệm phân biệt

⇒ u = 8; -v = -3 hoặc u = -3; -v = 8

⇒ u = 8; v = 3 hoặc u = -3; v = -8.