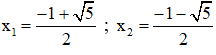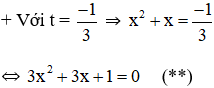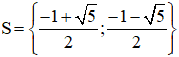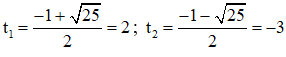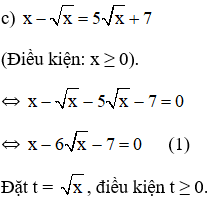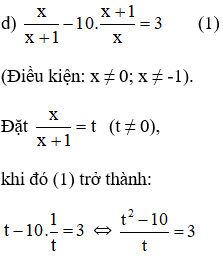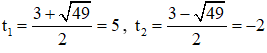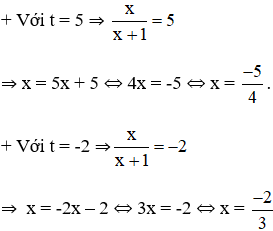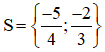Giải phương trình bằng cách đặt ẩn phụ: a) 3.(x^2 + x)^2 – 2(x^2 + x) – 1 = 0

* Hướng dẫn giải

a)

$3·{\left(x^2+x\right)}^2-2\left(x^2+x\right)-1=0\left(1\right)$

Đặt $t = x^2 + x,$

Khi đó (1) trở thành : $3t^2 – 2t – 1 = 0 \left(2\right)$

Giải (2) : Có a = 3 ; b = -2 ; c = -1

⇒ a + b + c = 0

⇒ (2) có hai nghiệm $t_1 = 1; t_2 = c/a = -1/3.$

+ Với t = 1 $\Rightarrow x^2 + x = 1 \iff x^2 + x – 1 = 0 (*)$

Có a = 1; b = 1; c = -1 $\Rightarrow \Delta = 1^2 – 4.1.(-1) = 5 > 0$

(*) có hai nghiệm

Có a = 3; b = 3; c = 1 ⇒$\Delta = 3^2 – 4.3.1 = -3 < 0$

⇒ (**) vô nghiệm.

Vậy phương trình (1) có tập nghiệm 

b)

$\begin{array}{l}{\left(x^2-4x+2\right)}^2+x^2-4x-4=0\\ \iff {\left(x^2-4x+2\right)}^2+x^2-4x+2-6=0\left(1\right)\end{array}$

Đặt $x^2 – 4x + 2 = t,$

Khi đó (1) trở thành:$t^2 + t – 6 = 0 \left(2\right)$

Giải (2): Có a = 1; b = 1; c = -6

⇒ $\Delta = 1^2 – 4.1.(-6) = 25 > 0$

⇒ (2) có hai nghiệm

+ Với t = 2 $\Rightarrow x^2 – 4x + 2 = 2$

$\iff x^2 – 4x = 0$

⇔ x(x – 4) = 0

⇔ x = 0 hoặc x = 4.

+ Với t = -3 $\Rightarrow x^2 – 4x + 2 = -3$

⇔ x2 – 4x + 5 = 0 (*)

Có a = 1; b = -4; c = 5 $\Rightarrow \Delta ’ = {(-2)}^2 – 1.5 = -1 < 0$

⇒ (*) vô nghiệm.

Vậy phương trình ban đầu có tập nghiệm S = {0; 4}.

Khi đó (1) trở thành: $t^2 – 6t – 7 = 0 \left(2\right)$

Giải (2): Có a = 1; b = -6; c = -7

⇒ a – b + c = 0

⇒ (2) có nghiệm $t_1 = -1; t_2 = -c/a = 7.$

Đối chiếu điều kiện chỉ có nghiệm t = 7 thỏa mãn.

+ Với t = 7 ⇒ √x = 7 ⇔ x = 49 (thỏa mãn).

Vậy phương trình đã cho có nghiệm x = 49.

$\iff t^2 – 10 = 3t \iff t^2 – 3t – 10 = 0 \left(2\right)$

Giải (2): Có a = 1; b = -3; c = -10

$\Rightarrow \Delta = {(-3)}^2 - 4.1.(-10) = 49 > 0$

⇒ (2) có hai nghiệm:

Cả hai nghiệm đều thỏa mãn điều kiện xác định.

Vậy phương trình đã cho có tập nghiệm