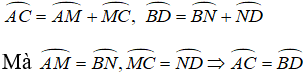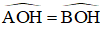Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Giải bài tập SGK Toán 9 tập 2 hay nhất Bài 2: Liên hệ giữa cung và dây !!
Chứng minh rằng: trong một đường tròn, hai cung bị...
Chứng minh rằng: trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
Câu hỏi :
Chứng minh rằng: trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
* Đáp án
* Hướng dẫn giải
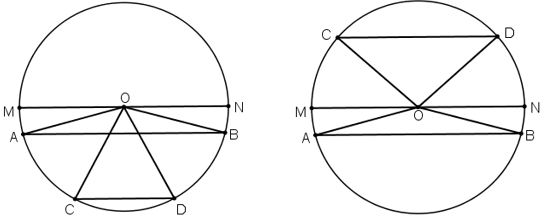
Vẽ đường tròn tâm O, các dây cung AB // CD.
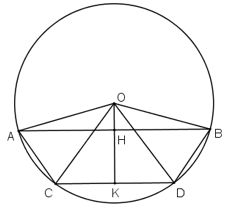
Cần chứng minh
Cách 1:
Kẻ bán kính MN // AB // CD
MN // AB
+ TH1: AB và CD cùng nằm trong một nửa đường tròn.
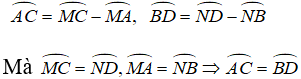
+ TH2: AB và CD thuộc hai nửa đường tròn khác nhau.
Cách 2:
Kẻ OH ⊥ AB; OK ⊥ CD (H ∈ AB, K ∈ CD)
Vì AB // CD ⇒ O, H, K thẳng hàng.
ΔOAB có OA = OB
⇒ ΔOAB cân tại O
⇒ đường cao OH đồng thời là đường phân giác
⇒
Chứng minh tương tự:
Kiến thức áp dụng
+ Trong một đường tròn, hai dây bằng nhau căng hai cung bằng nhau.
+ Trong cùng một đường tròn, hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau, tức là góc ở tâm chắn hai cung đó bằng nhau.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải bài tập SGK Toán 9 tập 2 hay nhất Bài 2: Liên hệ giữa cung và dây !!
Số câu hỏi: 7
Copyright © 2021 HOCTAP247