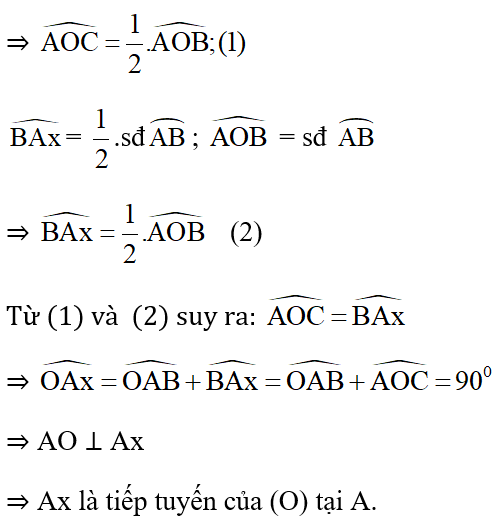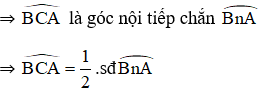Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Giải bài tập SGK Toán 9 tập 2 hay nhất Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung !!
Chứng minh định lí đảo của định lí về góc...
Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung
Câu hỏi :
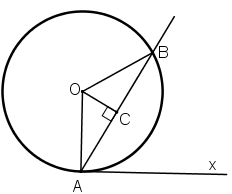
Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung , cụ thể là: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn(h.29).
* Đáp án
* Hướng dẫn giải
Cách 1: (Chứng minh trực tiếp)
Gọi C là chân đường cao hạ từ O xuống AB.
ΔOAB có OA = OB = R nên tam giác này cân tại O
⇒ đường cao OC đồng thời là phân giác
Cách 2: (Chứng minh phản chứng)
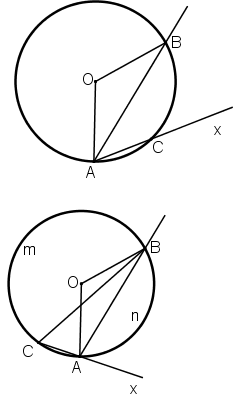
Giả sử Ax không phải tiếp tuyến của (O)
⇒ Ax là cắt (O) tại C khác A.
+ C nằm trên cung nhỏ AB
+ C nằm trên cung lớn AB
Mà 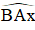
Vậy giả sử là sai ⇒ Ax là tiếp tuyến của đường tròn tâm O.
Kiến thức áp dụng
+ Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải bài tập SGK Toán 9 tập 2 hay nhất Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung !!
Số câu hỏi: 6
Copyright © 2021 HOCTAP247