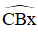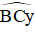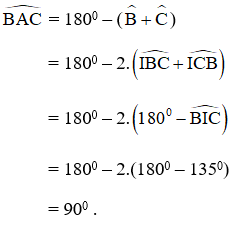Cho tam giác ABC vuông ở A, có cạnh BC cố định. Gọi I là giao điểm của ba
Câu hỏi :
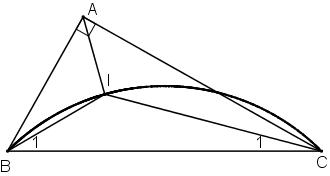
Cho tam giác ABC vuông ở A, có cạnh BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm I khi A thay đổi.
* Đáp án
* Hướng dẫn giải
* Dự đoán : Quỹ tích điểm I là cung chứa góc dựng trên đoạn BC.
* Chứng minh :
Phần thuận : Chứng minh mọi điểm I thỏa mãn điều kiện trên đều thuộc cung chứa góc dựng trên đoạn BC.
⇒ I thuộc cung chứa góc dựng trên đoạn thẳng BC.
Phần đảo: Chứng minh mọi điểm I thuộc cung chứa góc dựng trên đoạn BC, đều có tam giác ABC thỏa mãn điều kiện.
+ Lấy I trên cung chứa góc dựng trên đoạn BC
+ Kẻ tia Bx sao cho BI là phân giác của
+ Kẻ tia Cy sao cho CI là phân giác của
+ Bx cắt Cy tại A.
Khi đó I là giao điểm của hai đường phân giác trong tam giác ABC
Vậy ΔABC vuông tại A thỏa mãn đề bài.
Kết luận : Quỹ tích điểm I là toàn bộ cung chứa góc dựng trên đoạn BC (khác B và C).
Kiến thức áp dụng
+ Thông thường, bài toán quỹ tích ta làm theo các bước :
1, Dự đoán quỹ tích
2, Chứng minh quỹ tích : gồm Phần thuận và Phần đảo
3, Kết luận.
+ Quỹ tích các điểm M thỏa mãn 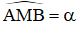
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải bài tập SGK Toán 9 tập 2 hay nhất Bài 6: Cung chứa góc !!
Copyright © 2021 HOCTAP247