Dựng tam giác ABC, biết BC = 4cm, góc A = 60o, bán kính đường tròn nội tiếp tam giác bằng 1cm.

* Hướng dẫn giải

Phân tích:

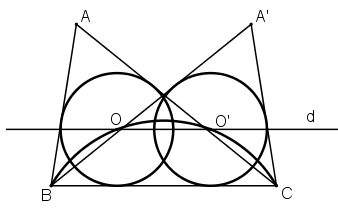
Giả sử dựng được ΔABC thỏa mãn điều kiện.

Gọi O là tâm đường tròn nội tiếp tam giác.

⇒ O thuộc cung m chứa góc 120º dựng trên đoạn BC.

+ Bán kính đường tròn nội tiếp ΔABC bằng 1

⇒ O cách BC 1cm

⇒ O thuộc d // BC và cách BC 1cm.

Vậy O là giao của cung m và đường thẳng d.

+ Khi đó ta dựng được đường tròn (O; 1) nội tiếp ΔABC

⇒ A là giao của tiếp tuyến đi qua B và C của đường tròn (O; 1).

Cách dựng:

+ Dựng BC = 4cm

+ Dựng đường thẳng (d) song song với BC và cách BC một khoảng là 1 cm.

+ Dựng cung m chứa góc 120º trên đoạn BC.

+ (d) cắt cung m tại O.

+ Dựng đường tròn tâm O, bán kính 1cm.

+ Kẻ tiếp tuyến từ B và C đến (O; 1cm).

Hai tiếp tuyến cắt nhau tại A.

ΔABC là tam giác cần dựng.

Chứng minh:

+ Theo cách dựng có BC = 4cm .

+ O thuộc cung 120º dựng trên đoạn BC

+ A là giao của 2 tiếp tuyến

⇒ (O; 1cm) tiếp xúc với AB và AC

Mà khoảng cách từ O đến BC = 1cm

⇒ (O; 1cm) cũng tiếp xúc với BC

⇒ (O; 1cm) là đường tròn nội tiếp ΔABC

Vậy ΔABC có BC = 4cm, 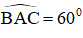 , đường tròn nội tiếp có bán kính 1cm thỏa mãn yêu cầu.

Biện luận:

Vì d cắt m tại hai điểm nên bài toán có hai nghiệm hình ΔABC và ΔA’BC như hình vẽ.