Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Trắc nghiệm Toán 9 Bài 2 (có đáp án): Tỉ số lượng giác của góc nhọn (phần 2) !!
Cho tam giác nhọn ABC hai đường cao AD và...
Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H
Câu hỏi :
Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H. Biết HD:HA = 3:2. Khi đó bằng?
A. 3
B. 5
C.
D.
* Đáp án
* Hướng dẫn giải
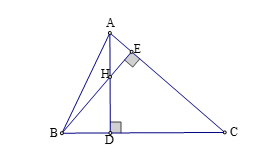
Xét tam giác vuông ABD và ADC, ta có: ;
Suy ra: (1)
Lại có (cùng phụ với ) và
Do đó (g.g), suy ra , do đó BD.DC = DH.AD (2)
Từ (1) và (2) suy ra (3)
Theo giả thiết suy ra hay , suy ra AD = HD
Thay vào (3) ta được:
Đáp án cần chọn là: D
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Toán 9 Bài 2 (có đáp án): Tỉ số lượng giác của góc nhọn (phần 2) !!
Số câu hỏi: 49
Copyright © 2021 HOCTAP247
