Cho một tam giác đều ABC có cạnh AB = 8cm, đường cao AH. Khi đó thể tích hình cầu.

* Hướng dẫn giải

Đáp án cần chọn là: C.

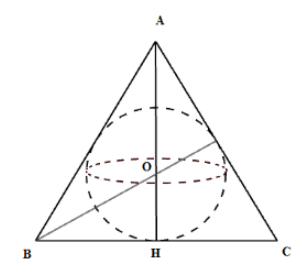
Vì ABC là tam giác đều nên tâm đường tròn nội tiếp trùng với trọng tâm O của tam giác

Khi đó bán kính đường tròn nội tiếp R = OH = $\frac{AH}{3}$

Xét tam giác vuông ABH có: $A{H}^2=A{B}^2-B{H}^2=a^2-{\left(\frac{a}{2}\right)}^2=\frac{3a^2}{4}\Rightarrow AH=\frac{a\sqrt{3}}{2}$

Suy ra R = $\frac{a\sqrt{3}}{6}$.

Khi quay nửa đường tròn nội tiếp tam giác ABC một vòng quanh AH ta được hình cầu bán kính R = $\frac{a\sqrt{3}}{6}$ $\Rightarrow$ V = $\frac{4}{3}{\mathrm{\pi R}}^3=\frac{4}{3}\mathrm{\pi }{\left(\frac{\mathrm{a}\sqrt{3}}{6}\right)}^3=\frac{\sqrt{3}{\mathrm{\pi a}}^3}{54}$

Chú ý: Một số em có thể nhớ sai công thức thể tích hình cầu thành $V={\mathrm{\pi R}}^3$ dẫn đến tính toán ra đáp án B sai.