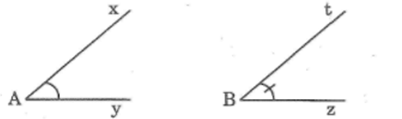Chương 2: Góc
Chương 2: Góc
Hãy kể tên một số hình ảnh của mặt phẳng.
Hãy gấp một tờ giấy. Trải tờ giấy lên mặt bàn rồi quan sát xem nếp gấp có phải là hình ảnh bờ chung của hai nửa mặt phẳng đối nhau hay không?
Điền vào chỗ trống trong các phát biểu sau:
a) Bất kì đường thẳng nào nằm trên mặt phẳng cũng là bờ chung của hai nửa mặt phẳng…
b) Cho ba điểm không thẳng hàng 0,A,B. Tia Ox nằm giữa hai tia OA,OB khi tia Ox cắt ….
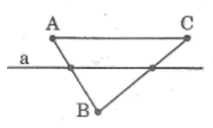
Cho ba điểm A, B, C không thẳng hàng. Vẽ đường thẳng a cắt các đoạn thẳng AB, AC và không đi qua A,B,C.
a) Gọi tên hai nửa mặt phẳng đối nhau bờ a,
b) Đoạn thẳng BC có cắt đường thẳng a hay không?
Gọi M là điểm nằm giữa hai điểm A, B lấy điểm O không nằm trên đường thẳng AB. Vẽ ba tia OA,OB,OM.
Hỏi tia nào nằm giữa hai tia còn lại?
Điền vào chỗ trống trong các phát biểu sau:
a) Hình gồm hai tia chung gốc Ox, Oy là ..... Điểm O là.... Hia tia Ox, Oy là...
b) Góc RST có đỉnh là ....., Có cạnh là ....
c) góc bẹt là .....
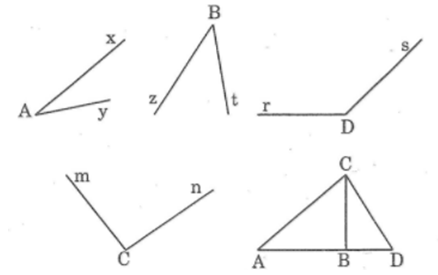
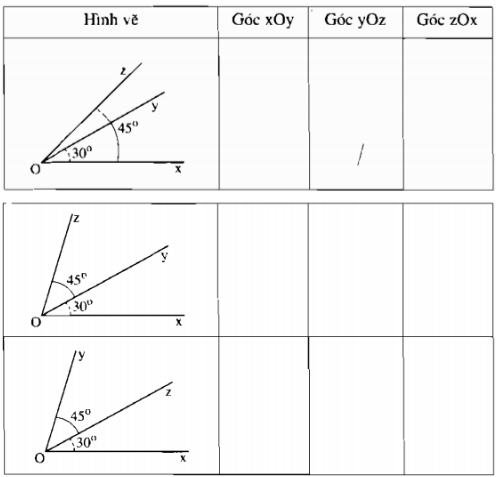
Quan sát hình 7 rồi điền vào bảng sau:
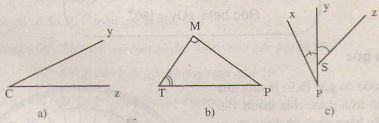
|
Hình |
Tên góc (cách viết thông thường) |
Tên đỉnh |
Tên cạnh |
Tên góc (Cách viết kí hiệu) |
|
a |
Góc yCz, góc zCy, góc C |
C |
Cy,Cz |
\(\widehat{yCz};\widehat{zCy},\widehat{C}\) |
|
b |
……………………… |
… |
…………………… |
……………………. |
|
c |
……………………….. |
... |
…………………… |
…………………….. |
Đọc và kí hiệu tên các góc ở hình 8. Có tất cả bao nhiêu góc ?
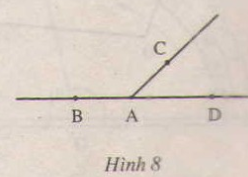
Điền vào chỗ trống trong các phát biểu sau:
Khi hai tia Oy, Oz không đối nhau, điẻm A ngằm trong góc yOz nằm giữa hai tia..... .
Lấy ba điểm không thẳng hàng A,B,C.
Gạch chéo phần mặt phẳng chứa tất cả các điểm trong cả 3 góc BAC, ACB,CBA.
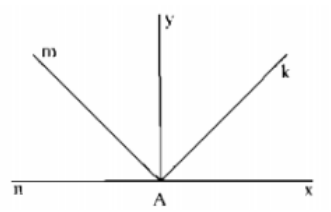
Nhìn hình 18 Đọc số đo của các góc xOy, xOz, xOt.
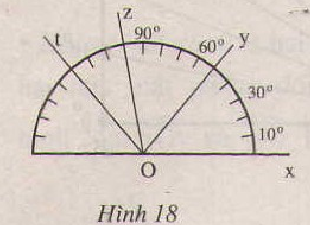
Đo các góc BAC, ABC, ACB ở hình 19. So sánh các góc ấy'
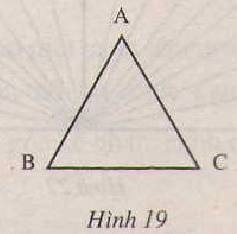
Đo các góc ILK, IKL, LIK ở hình 20
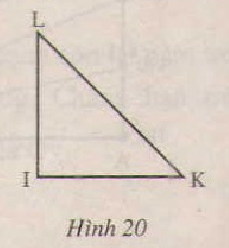
Xem hình 21. Ước lượng bằng mắt xem góc nào vuông, nhọn,tù ,bẹt.
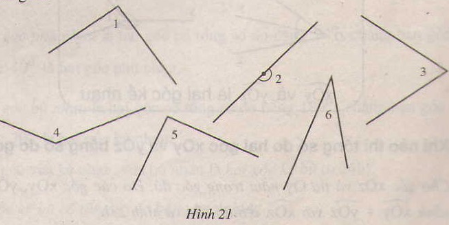
Dùng góc vuông của êke để kiểm tra lại kết quả. Dùng thước đo góc tìm số đo mỗi góc.
Ta có thể xem kim phút và kim giờ của đồng hồ là hai tia chung gốc(Gốc trùng với trục quay của hai kim). Tại mỗi thời điểm hai kim tạo thành một góc. Tìm số đo của góc đó lúc 2 giờ, 3 giờ, 5 giờ, 10 giờ.
Khi hai tia Ox, Oy trùng nhau, trong trường hợp cần thiết, ta cũng gọi xOy là một góc và gọi là "Góc không". Số đo của góc là \(0^{0}\). Tìm số đo của góc tạo bởi kim giờ và kim phút lúc 12 giờ.
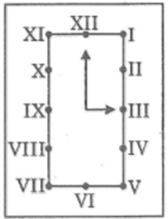
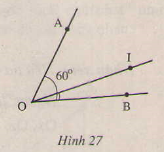
Đố: Một em học sinh đề nghị làm một thước đo góc hình chữ nhật như hình 22, cac s đoạn thẳng trên các cạnh BC,CD,DA có độ dài bằng nhau.
Hãy đo để kiểm tra xem thước đó đúng hay sai.
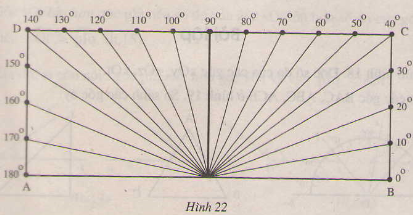
Hình 25 cho biết tia OA nằm giữa hai tia OB và OC, \(\widehat{BOA}= 45^{0}, \widehat{AOC}= 32^{0}\). Tính \(\widehat{BOC}\). Dùng thước đo góc để kểm tra lại,
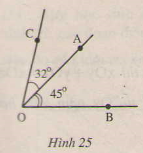
Hình 26 cho biết hai góc kề bù xOy và yOy', \(\widehat{xOy} = 120^{0}\) . Tính \(\widehat{yOy'}\)
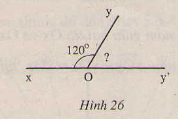
Hình 27 cho biết ia OI nằm giữa hai tia OA, OB, \(\widehat{AOB}= 60^{0}, \widehat{BOI}= \frac{1}{4}\widehat{ AOB}\). Tính Số đo góc BOI và AOI.
a) Đo các góc ở hình 28a,b.
b) Viết tên các cặp góc phụ nhau ở hình 28b.
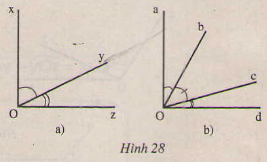
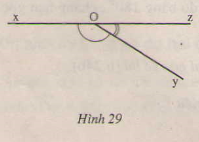
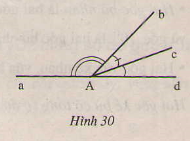
a) Đo các góc ở hình 29,30.
b) Viết tên các góc bù nhau ở hình 30.
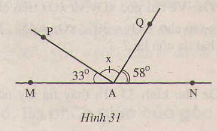
Hình 31 cho biết hai tia AM và AN đối nhau,\(\widehat{MAP}= 22^{0} , \widehat{NAQ}= 58^{0}\) góc tia AO nằn giữa hai tia AN và AP , Hãy tính số đo x của \(\widehat{PAD}\)
Vẽ góc xBy có số đo bằng 450
Hướng dẫn: Vẽ tia Bx, sau đó trên một nửa mặt bẳng có bờ chứa tia Bx vẽ tia By sao cho = 450
Vẽ góc IKM có số đo bằng 1350
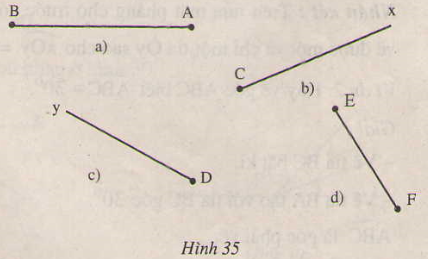
Vẽ góc cho biết một cạnh và số đo góc đó trong bốn trường hợp sau(h.35)
a) \(\widehat{BAC}\) = 200
b) \(\widehat{ xCz}\) = 1100
c) \(\widehat{ yDx}\) = 800
d) \(\widehat{ EFy}\) = 1450
Trên cùng một mặt phẳng bờ chứa tia OA, vẽ hai tia OB, OC sao cho
\(\widehat{BOA}\)= 1450 , \(\widehat{COA}\)=
Tính số đo góc BOC.
Trên mặt phẳng, cho tia Ax. Có thể vẽ được mấy tia Ay sao cho \(\widehat{xAy}\) = 500
Gọi Ot, Ot' là hai tia nằm trên cùng một nửa mặt phẳng bờ là đường thẳng xy đi qua O. Biết \(\widehat{xOt}\) = 300 , \(\widehat{yOt'}\) = 600. Tính số đo các góc yOt, tOt'.
Trên cùng một nửa mặt phẳng chứa bờ Ox, vẽ tia Ot sao cho góc \(\widehat{xOt}\)=250 , \(\widehat{xOy}\)= 500.
a) Tia Ot có nằm giữa hai tia Ox và Oy không?
b) So sánh góc tOy và góc xOt.
c ) Tia Ot có là tia phân giác của góc xOy không? Vì sao?
a) Vẽ góc xOy có số đo 1260
b) vẽ tia phân giác của góc xOy ở câu a.
Khi nào ta kết luận được tia Ox là tia phân giác của góc xOy? Trong những câu trả lời sau, em hay chọn những câu đúng:
a) \(\widehat{xOt}\) = \(\widehat{yOt}\)
b)\(\widehat{xOt}\) + \(\widehat{tOy}\) = \(\widehat{xOy}\)
c) \(\widehat{xOt}\) +\(\widehat{tOy}\) = \(\widehat{xOy}\) và \(\widehat{xOt}\) =\(\widehat{yOt}\)
d) \(\widehat{xOt}\) =\(\widehat{yOt}\) = \(\frac{1}2\widehat{xOy}\)
Vẽ hai góc kề bù xOy, yOx', biết \(\widehat{xOy}\) = 1300.Gọi Ot là tia phân giác của góc xOy. Tính số đo góc \(\widehat{x'Ot}\).
Vẽ hai góc kề bù xOy và yOx', biết \(\widehat{xOy}\) = 1000 . Gọi Ot là thia phân giác của góc xOy và Ot' là tia phân giác của góc x'Oy. Tính số đo các góc x'Ot, xOt', tOt'.
Vẽ góc bẹt xOy. Vẽ tia phân giác Om của góc đó. Vẽ tia phân giác Oa của góc xOm. Bẽ tia phân giác Ob của góc mOy. Tính số đo góc aOb.
Cho hai tia Oy,Oz cùng nằm trên một nửa mặt phẳng có bờ chứa tia Ox. Biết:
\(\widehat{ xOy}\)=300,\(\widehat{ xOz}\)=800
Vẽ tia phân giác Om của góc xOy. Vẽ tia phân giác On của yOz. Tính
Cho hai tia Oy, Oz cùng nằm trên một nửa mặt phẳng có bờ chứa tia Ox. Biết rằng \(\widehat{xOy}\)=300 , \(\widehat{xOz}\)= 1200.
a) Tính số đo góc yOz.
b) Vẽ tia phân giác Om của \(\widehat{xOy}\),tia phân giác On của \(\widehat{xOz}\). Tính số đo góc mOn
Trong hình 48, ta có hai đường tròn(O;2cm) và (A;2cm) cắt nhau tại C,D. Điểm A nằm trên đường tròn tâm O.
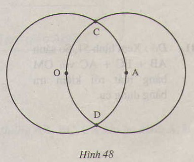
a) Vẽ đường tròn tâm C, bán kính 2cm.
b) Vì sao đường tròn(C;2cm) đi qua O,A?
Trên hình 49, ta có hai đường tròn (A;2cm) và (B;2cm) cắt nhau tại C,D, AB=4cm. Đường tròn tâm A,B lần lượt cắt đoạn thẳn AB tại K,I.

a) Tính CA, CB,DA,DB.
b) I có phải là trung điểm của đoạn thẳng AB không?
c) Tính IK.
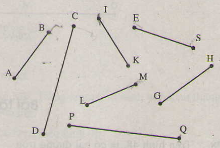
Với compa, hãy so sánh các đoạn thẳng trong hình 50 rồi đánh cùng một dấu cho các đoạn thẳng bằng nhau.
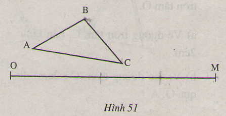
Đố: Xem hình 51. So sánh AB+BC+AC với OM bằng mắt rồi kiểm tra bằng dụng cụ.
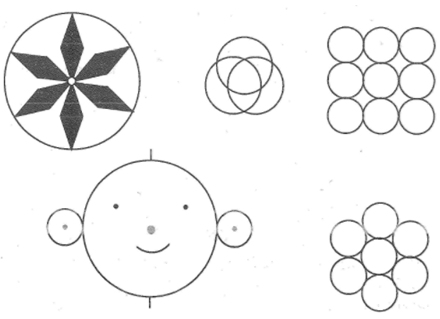
Vẽ lại các hình sau(đúng kích thước như hình đã cho)
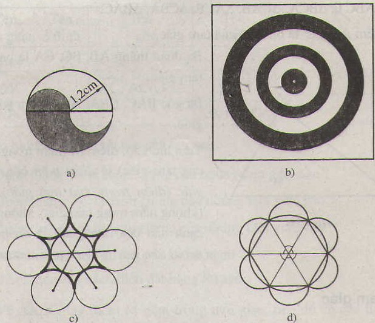
Điền vào chỗ trống trong các phát biểu sau:
a) Hình tạo thành bởi ....... được gọi là tam giác MNP.
b) Tam giác TUV là hình.............. .
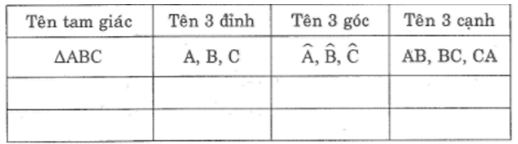
Xem hình 55 rồi điền vào bảng sau:
|
Tên tam giác |
Tên 3 đỉnh |
Tên 3 góc |
Tên 3 cạnh |
|
\(\Delta\)ABI |
A,B,I |
|
|
|
\(\Delta\)AIC |
|
\(\widehat{IAC},\widehat{ACI},\widehat{CIA}\) |
|
|
\(\Delta\)ABC |
|
|
AB, Bc, CA |
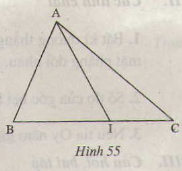
Xem hình 55 rồi trả lời các câu hỏi sau.
a) Đoạn thẳng AI là cạnh chung của những tam giác nào?
b) Đoạn thẳng AC là cạnh chung của nhưng tam giác nào?
c) Đoạn thẳng AB là cạnh chung của những tam giác nào?
d) Hai tam giác nào có hai góc kề bù nhau?
Vẽ hình theo các cách diễn đạt bằng lời sau:
a) vẽ tam giác ABC, lấy điểm M nằm trong tam giác, tiếp đó vẽ các tia AM, BM,CM.
b) vẽ tam giác IKM, lấy điểm A nằm trên cạnh KM, điểm B nằm cạnh IM. Vẽ giao điểm N của hai đoạn thẳng IA,KB.
Vẽ đoạn thẳng IR dài 35cm. Vẽ một điểm T sao cho TI=2,5 cm, TR=2cm. Vẽ tam giác TIR.
Cho ba điểm A, B, C nằm ngoài đường thẳng a. Biết rằng cả hai đoạn thẳng BA, BC đều cắt đường thẳng a. Hỏi đoạn thắng AC có cắt đường thẳng a hay không? Vì sao?
Gọi tên hai nửa mặt phẳng đối nhau bờ a.
Cho bốn điển A, B, C, D không nằm trên đường thẳng a, trong đó A và B thuộc cùng một nửa mặt phẳng bờ a, còn C và D thuộc nửa mặt phẳng kia.Hỏi đường thẳng a cắt đoạn thẳng nào, không cắt đoạn thẳng nào trong các đoạn thẳng nối hai trong bốn điểm A, B, C, D?
Cho hai tia Oa, Ob không đối nhau. Lấy các điểm A và B không trùng O sao cho A thuộc tia Oa, B thuộc tia Ob . Gọi C là điểm nằm giữa A và B. Vẽ điểm D sao cho B nằm giữa A và D. Hỏi trong hai tia OC, OD thì tia nào nằm giữa hai tia OA, OB, tia nào không nằm giữa hai tia OA, OB?
Cho hai tia Oa, Ob không đối nhau. Lấy các điểm A và B không trùng O sao cho A thuộc tia Oa, B thuộc tia Ob. Gọi C là điểm nằm giữa A, và B. Gọi M là điểm không trùng O thuộc tia đối của tia OC.
a) Tia OM có cắt đoạn thẳng AB hay không?
b) Tia OB có cắt đoạn thẳng AM hay không?
c) Tia OA có cắt đoạn thẳng BM hay không?
d) Trong ba tia OA, OB, OM có tia nào nằm giữa hai tia còn lại hay không?
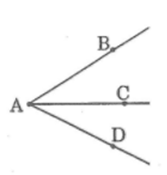
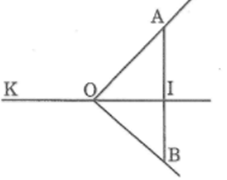
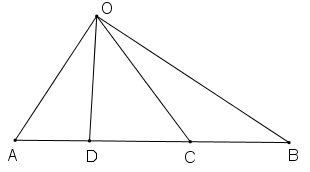
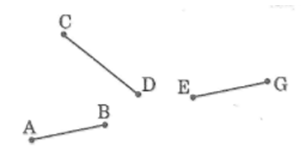
Ở hình bên, cho ba điểm A, B, C thẳng hàng.
a) Gọi tên hai tia đối nhau.
b) Tia BE nằm giữa hai tia nào?
c) Tia BD nằm giữa hai tia nào?
Vẽ hình theo cách diễn đạt bằng lời trong mỗi trường hợp dưới đây
a) Nửa mặt phẳng (I) có bờ là đường thẳng I
b) Điểm M thuộc nửa mặt phẳng có bờ là đường thẳng d và điểm N thuộc nửa mặt phẳng đối.
c) Điểm M thuộc nửa mặt phẳng có bờ là đường thẳng a. Hai điểm M. N nằm khác phía đối với đường thẳng a. Hai điểm N, P nằm khác phía đối với đường thẳng a
d) Hai đường thẳng m và n cắt nhau tại điểm O. Điểm A thuộc nửa mặt phẳng bờ là đường thẳng m. Hai điểm A, B ở cùng phía với đường thẳng m nhưng khác phía đối với đường thẳng n. Điểm C vừa thuộc nửa mặt phẳng bờ n có chứa điểm B vừa thuộc nửa mặt phẳng bờ m không chứa điểm A. Điểm D không thuộc nửa mặt phẳng bờ n có chứa điểm B và hai điểm A, D khác phía đối với đường thẳng m.
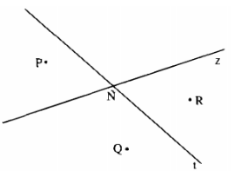
Dựa vào hình bs.1 nối mỗi ý ở cột A với chỉ một ý ở cột B để được kết quả đúng.
- Cột A
1) Hai điểm P,Q
2) Hai điểm P, R
3) Hai điểm Q,R
- Cột B
a) thuộc nửa mặt phẳng có bờ là đường thẳng z, nằm khác phía đối với đường thẳng t
b) thuộc nửa mặt phẳng có bờ là đường thẳng t và thuộc nửa mặt phẳng có bờ là đường thẳng z
c) nằm khác phía đối với đường thẳng z và cũng nằm khác phía đối với đường thẳng t
d) thuộc hai nửa mặt phẳng đối nhau có bờ là đường thẳng z và cùng thuộc nửa mặt phẳng có bờ là đường thẳng t
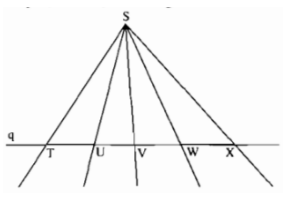
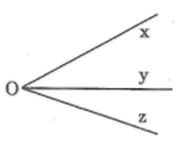
Nhìn hình bs.2 hãy đọc tên một tia nằm giữa hai tia khác.
Đọc tên và viết ký hiệu các góc ở hình bên:
Có bao nhiêu góc tất cả?
Vẽ ba tia chung gốc Ox, Oy, Oz. Kí hiệu các góc có được là \(\widehat {{O_1}}\); \(\widehat {{O_2}}\); \(\widehat {{O_3}}\)
| Góc | Tên đỉnh | Têm cạnh |
| \(\widehat {{O_1}}\) | ||
| \(\widehat {{O_2}}\) | ||
| \(\widehat {{O_3}}\) |
Bổ sung chỗ thiếu (…) trong các phát biểu sau:
a) Góc xOy là hình gồm ……………
b) Góc yOz được ký hiệu là…………
c) Góc bẹt là góc có ………
Bổ sung phần thiếu (…) trong phát biểu sau:
Khi hai tia Ox, Oy không đối nhau, M là điểm nằm trong góc xOy nếu …………
Vẽ:
a) Góc xOy.
b) Tia OM nằm trong góc xOy.
c) Điểm N nằm trong góc xOy.
Nhìn và đọc tên góc, tên đỉnh, tên các cạnh, viết ký hiệu của mỗi góc có trong hình bs.3
Vẽ hình theo cách diễn đạt bằng lời trong mỗi trường hợp sau đây
a) Vẽ góc xOy không phải là góc bẹt;
b) Vẽ góc bẹt tBz;
c) Vẽ góc jGk và điểm M nằm bên trong góc đó;
d) Vẽ góc nCm và nCt sao cho tia Cm nằm giữa hai tia Cn và Ct;
e) Vẽ các góc xOy, yOz, zOt sao cho tia Oz nằm trong góc xOy, tia Oy nằm trong góc zOt và xOt là góc bẹt.
Mỗi câu sau đây đúng hay sai?
a) Hình taọ bở hai tia là một góc;
b) Hình tạo bởi hai tia phân biệt là một góc;
c) Hình tạo bởi hai tia cắt nhau là một góc;
d) Hình tạo bởi hai tia trùng nhau là một góc;
e) Hình tạo bởi hai tia đối nhau là một góc;
f) Hình tạo bởi hai tia bất kỳ trên một đường thẳng là một góc bẹt;
g) Hình tạo bởi hai tia có nhiều điểm chung (nhưng không trùng nhau) là một góc bẹt;
h) Hình tạo bởi hai tia trùng nhau là một góc bẹt;
i) Khi vẽ hai góc xOy và yOz thì Oy luôn nằm trong góc xOz;
j) Khi vẽ hai góc mOn và nOt, điểm bất kỳ thuộc tia On (không trùng với O) luôn nằm trong góc mOt
k) Cho góc pQr (không phải là góc bẹt), điểm A bất kỳ trên tia Qp, điểm B bất kỳ trên tia Qr (A và B không trùng với Q). Điểm M thuộc đoạn thẳng AB. Khi đó tia QM luôn nằm trong góc pQr.
Xem hình dưới đây:
a) Ước lượng bằng mắt số đo mỗi góc rồi ghi vào bảng.
b) Dùng thước đo góc tìm số đo mỗi góc rồi ghi vào bảng.
c) Sắp xếp các góc theo thứ tự lớn dần.
| Tên góc | Số đo ước lượng | Số đo bằng thước |
| \(\widehat {xAy}\) | ||
| \(\widehat {mCn}\) | ||
| ... |
Một học sinh làm một mặt đồng hồ như hình 4. Hãy đo để kiểm tra xem đồng hồ đó kẻ đúng hay sai?
Hỏi lúc mấy giờ đúng thì kim phút và kim giờ của đồng hồ tạo thành góc 00, 600, 900, 1500, 1800?
Đo các góc CED, CGD, BED, DCE ở hình dưới
Đổi thành độ, phút:
15,250 = 15\({\frac{1}{4}^0}\) = 15015’ = 915’
30,50= …..=…..=…..
60,750= …..=…..=…..
90,20= …..=…..=…..
45,150= …..=…..=…..
Hãy cho biết mỗi câu sau đây là đúng hay sai?
a) Góc có số đo 1350 là góc nhọn;
b) Góc có số đo 750 là góc tù;
c) Góc có số đo 900 là góc bẹt;
d) Góc có số đo 1800 là góc vuông;
e) Một góc không phải là góc tù thì phải là góc nhọn;
f) Một góc không phải là góc vuông thì phải là góc tù;
g) Một góc bé hơn góc bẹt thì phải là góc tù;
h) Góc nhỏ hơn 1v là góc nhọn;
i) Góc tù nhỏ hơn góc bẹt.
Cho hình bs.4
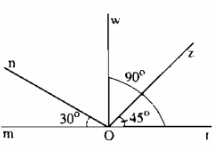
a) Hãy đọc tên các góc đỉnh O có trong hình đó;
b) Cho biết số đo của góc nhọn đỉnh O, một cạnh là Ot có trong hình đó;
c) Cho biết số đo của góc nhọn đỉnh O, một cạnh Om có trong hình đó;
d) Hãy đo và cho biết tên của các góc vuông đỉnh O có trong hình đó;
e) Cho biết số đo của các góc tù đỉnh O có trong hình đó;
f) Hãy đo và cho biết tên của góc bẹt đỉnh O có trong hình đó.
a) Hai đường thẳng xx’, yy’ cắt nhai tại điểm O và \(\widehat {xOy} = {90^0}\). Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox.
b) Hai đường thẳng xx’, yy’ cắt nhai tại điểm O và \(\widehat {xOy} = {30^0}\). Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox.
Gọi Oz là tia nằm giữa hai tia Ox, Oy. Biết \(\widehat {xOy} = {a^0},\widehat {zOx} = {b^0}\). Tính \(\widehat {yOz}\)
Cho biết \(\widehat {LPM} = {90^0}\). Vẽ tia PU để \(\widehat {LPM} = \widehat {LPU} + \widehat {UPM}\)
Ở hình dưới, hai tia OI , OK đối nhau. Tia OI cắt đoạn thẳng AB tại I. Biết \(\widehat {KOA} = {120^0},\widehat {BOI} = {45^0}\)
Tính \(\widehat {KOB},\widehat {AOI},\widehat {BOA}\)
Xem hình dưới, làm thế nào để chỉ đo hai góc mà biết được số đo của cả ba góc xOy, xOz, yOz
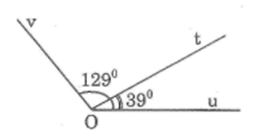
Xem hình dưới. Hỏi \(\widehat {tOv}\) có phải là góc vuông hay không? Vì sao?
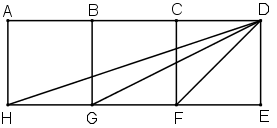
Xem hình dưới:
a) Đo góc DHE , DGE , DFE
b) Hỏi \(\widehat {DFE}\) có bằng \(\widehat {DGE}\) + \(\widehat {DHE}\) hay không ?
Tia Oy nằm giữa hai tia Ox và Oz. Biết \(\widehat {xOy} = {40^0}\). Hỏi góc xOz là nhọn, vuông, tù hay bẹt nếu số đo của góc yOz lần lượt bằng 300, 500, 700, 1400
Trên đường thẳng d từ trái sang phải ta lấy các điểm A, D, C, B và lấy điểm O nằm ngoài đường thẳng d.
Biết: \(\widehat {AOD} = {30^0}\), \(\widehat {DOC} = {40^0}\); \(\widehat {AOB} = {90^0}\). Tính \(\widehat {AOC},\widehat {COB},\widehat {DOB}\)
Nhìn mỗi hình vẽ và điền đúng số đo góc vào ô còn trống trong bảng sau
Cho hình bs.5
a) Gọi tên các cặp góc kề nhau đỉnh O trong hình đó.
b) Cho biết số đo của các góc đỉnh O trong hình đó.
c) Cho biết những cặp góc phụ nhau đỉnh O.
d) Cho biết những cặp góc bù nhau đỉnh O.
e) Cho biết những cặp góc kề bù nhau đỉnh O
Mỗi câu sau đây là đúng hay sai?
a) Ta luôn có \(\widehat {mOt} + \widehat {wOt} = \widehat {mOw}\)
b) Nếu \(\widehat {mOt} + \widehat {wOt} = \widehat {mOw}\) thì tia Ot nằm giữa hai tia Om và Ow;
c) Hai góc có tổng bằng 1800 là hai góc kề bù;
d) Hai góc kề bù nếu tia đối của góc này là tia đối của góc kia;
e) Hai góc nhọn là hai góc phụ nhau;
f) Hai góc nhọn là hai góc bù nhau;
g) Hai góc vuông là hai góc kề bù;
h) Hai góc phụ nhau mà một góc là 450 thì góc kia là 1350
i) Hai góc bù nhau mà một góc là 450 thì góc kia là 450
Vẽ góc xOl có số đo bằng 400
Vẽ góc vuông BAC.
Hướng dẫn:
Cách 1: Dùng thước đo góc.
Cách 2: Dùng êke
So sánh hai góc ở hình dưới.
Hướng dẫn:
Cách 1: Đo riêng từng góc rồi so sánh hai số đó
Cách 2: Vẽ lại hai góc lên giấy trong. Đặt chồng hai góc sao cho đỉnh trùng nhau, một cạnh trùng nhau, hai cạnh còn lại của hai góc nằm cùng phía đối với cạnh trùng nhau rồi vận dụng kiến thức bài 5 để kết luận.
Tính tổng số đo hai góc ở hình trong bài 26
Hướng dẫn:
Cách 1: Đo riêng từng góc rồi cộng hai số đo.
Cách 2: Vẽ hai góc ở vị trí kề nhau rồi đo góc tổng
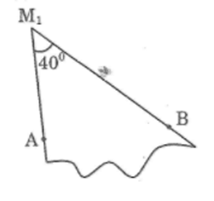
a) Vẽ góc 400 có đỉnh là M trên giấy cứng. Cắt ra ta được một mẫu hình.
b) Đóng hai chiếc đinh vào hai điểm A và B cách nhau 2,5 cm. Đưa mẫu hình vào khe hở giữa hai chiếc đinh sao cho một cạnh sát A, một cạnh sát B. Khi đó đỉnh M của góc ở vị trí M1. Đặt mẫu hình nhiều lần để được nhiều vị trí M1, M2, M3, ... khác nhau của đỉnh M. Vậy ta có:
\(\widehat {A{M_1}B}\) = \(\widehat {A{M_2}B}\) = \(\widehat {A{M_3}B}\) = … = 400
Đánh dấu khoảng 10 vị trí khác nhau của đỉnh M và dự đoán quỹ đạo của đỉnh M (hình bên)
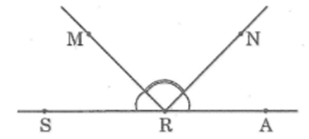
a) Vẽ vào vở hình dưới trong đó ba điểm S, R, A thẳng hàng và \(\widehat {ARM}\) = \(\widehat {SRN}\) = 1300
b) Tính \(\widehat {ARN}\), \(\widehat {MRS}\), \(\widehat {MRN}\)
c) Dùng thước đo góc kiểm tra lại kết quả
Vẽ liên tiếp các hình theo cách diễn đạt sau:
a) \(\widehat {nAx} = {180^0}\)
b) \(\widehat {mAx} = {135^0}\)
c) \(\widehat {kAx} = {45^0}\) tia Ak nằm trong góc xAm;
d) \(\widehat {nAy} = {90^0}\) , tia Ay nằm trong góc xAm.
Vẽ từng hình theo mỗi cách diễn đạt sau
a) Hai góc xOy và yOz kề bù, với \(\widehat {xOy} = {135^0}\)
b) Hai góc mOn và nOt kề nhau và phụ nhau, với \(\widehat {nOm} = {30^0}\)
c) Cho tia Ap. Vẽ \(\widehat {qAp} = {30^0}\).
d) Cho tia Ck. Vẽ \(\widehat {rBt} = {90^0}\)
e) Cho tia Ck. Vẽ \(\widehat {hCk} = {45^0}\)
Vẽ \(\widehat {mOn} = {30^0}\). Tiếp góc nOp kề bù với góc mOn. Vẽ tiếp góc pOq phụ với góc mOn đồng thời tia Oq nằm trong góc nOp. Cho biết số đo của góc nOq ?
a) Vẽ góc \(\widehat {xOy} = {44^0}\)
b) Vẽ tia phân giác Oz của góc ấy
Hướng dẫn: Cách 1: Dùng thước đo góc
Cách 2: Gấp giấy
a) Vẽ góc bẹt xOy.
b) Vẽ tia Ot sao cho \(\widehat {xOt} = {30^0}\)
c) Vẽ tia Oz sao cho \(\widehat {yOz} = {30^0}\) (Ot và Oz cùng nằm trên một nửa mặt phẳng bờ xy)
d) Vẽ tia phân giác Om của góc tOz
e) Vì sao tia Om cũng là tia phân giác của xOy ?
a) Cắt hai góc vuông rồi đặt lên nhau như hình dưới
b) Vì sao có \(\widehat {xOz} = \widehat {yOt}\)
c) Vì sao tia phân giác của yOz cũng là tia phân giác của góc xOt?
Cho hai tia Oy, Oz cùng nằm trong nửa mặt phẳng có bờ chứa tia Ox sao cho \(\widehat {xOy} = {80^0}\), \(\widehat {xOz} = {30^0}\). Gọi Om là tia phân giác của góc yOz. Tính \(\widehat {xOm}\)
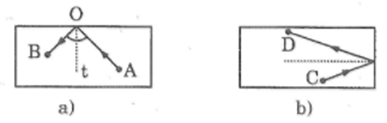
Trong trò chơi bi-a, các đấu thủ thường áp dụng kinh nghiệm sau: Muốn đẩy quả cầu A vào điểm O (trên cạnh bàn) để khi bắn ra trúng quả cầu B (Hình bên trái) thì cần xác định điểm O sao cho tia Ot (tia vuông góc với mặt bàn tại O) phải là tia phân giác của góc AOB.
Em hãy xem hình bên phải rồi dùng các dụng cụ đo (thước thẳng, êke, thước đo góc) kiểm tra xem quả cầu C sau khi đập vào cạnh bàn có đập trúng vào quả cầu D không?
Vẽ \(\widehat {xOy} = {50^0}\). Vẽ tiếp góc yOz kề bù với góc xOy. Vẽ tiếp Om là tia phân giác của góc xOy. Vẽ tiếp On là tia phân giác của góc yOz.
Dùng giả thiết trên cho các bài số 6.1, 6.2, 6.3, 6.4 sau đây. Hãy chọn kết quả đúng.
Số đo của góc xOn bằng
(A) 250
(B) 1150
(C) 900
(D) 650
Vẽ \(\widehat {xOy} = {50^0}\). Vẽ tiếp góc yOz kề bù với góc xOy. Vẽ tiếp Om là tia phân giác của góc xOy. Vẽ tiếp On là tia phân giác của góc yOz.
Dùng giả thiết trên cho các bài số 6.1, 6.2, 6.3, 6.4 sau đây. Hãy chọn kết quả đúng.
Số đo của góc xOm bằng
(A) 250
(B) 650
(C) 900
(D) 1150
Vẽ \(\widehat {xOy} = {50^0}\). Vẽ tiếp góc yOz kề bù với góc xOy. Vẽ tiếp Om là tia phân giác của góc xOy. Vẽ tiếp On là tia phân giác của góc yOz.
Dùng giả thiết trên cho các bài số 6.1, 6.2, 6.3, 6.4 sau đây. Hãy chọn kết quả đúng.
Số đo của góc mOn bằng
(A) 250
(B) 650
(C) 900
(D) 1150
Vẽ \(\widehat {xOy} = {50^0}\). Vẽ tiếp góc yOz kề bù với góc xOy. Vẽ tiếp Om là tia phân giác của góc xOy. Vẽ tiếp On là tia phân giác của góc yOz.
Dùng giả thiết trên cho các bài số 6.1, 6.2, 6.3, 6.4 sau đây. Hãy chọn kết quả đúng.
Số đo của góc mOz bằng
(A) 250
(B) 900
(C) 1150
(D) 1550
Mỗi câu sau đây là đúng hay sai?
a) Tia nằm trong góc xOy là tia phân giác của góc đó;
b) Tia tạo với một cạnh của góc xOy một góc bằng nửa số đo góc xOy là tia phân giác của góc đó;
c) Mỗi góc có duy nhất một tia phân giác;
Vẽ \(\widehat {mOn} = {120^0}\). Vẽ tiếp \(\widehat {mOt} = {90^0}\) sao cho tia Ot nằm trong góc mOn. Vẽ tiếp ∠(nOz) = 90o sao cho tia Oz nằm trong góc mOn. Vẽ tiếp Ox là tia phân giác của góc mOn.
a) Cho biết số đo của góc nOt.
b) Cho biết số đo của góc mOz;
c) Cho biết số đo của góc zOx.
Vẽ \(\widehat {mOn} = {160^0}\). Vẽ tiếp \(\widehat {mOt} = {120^0}\) sao cho tia Ot nằm trong góc mOn. Vẽ tiếp \(\widehat {zOt} = {80^0}\) sao cho tia Oz nằm trong góc mOt. Vẽ tiếp Ox là tia phân giác của góc mOn.
a) Dùng kết quả đo đạc để khẳng định các góc mOz, zOx, xOt, tOn bằng nhau.
b) Dùng kết quả đo đạc để khẳng định Ox là tia phân giác của góc zOt.
Cho hai điểm A,B cách nhau 3cm. Vẽ đường tròn (A; 2,5cm) và đường tròn (B; 1,5cm). Hai đường tròn này cắt nhau tại C và D
a) Tính CA, DB.
b) Tại sao đường tròn (B; 1,5cm) cắt đoạn thẳng AB tại trung điểm I của AB?
c) Đường tròn (A; 2,5cm) cắt đoạn thẳng AB tại K. Tính KB
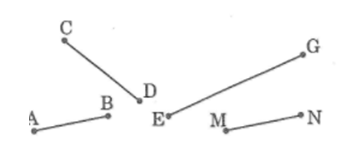
So sánh các đoạn thẳng trong hình bên bằng mắt rồi kiểm tra kết quả bằng compa.
Làm thế nào để chỉ đo một lần, mà biết được tổng độ dài các đoạn thẳng ở hình bên .
a) Vẽ đoạn thẳng AB bằng 3cm.
b) Vẽ đường tròn tâm A bán kính 2cm.
c) Vẽ đường tròn tâm B bán kính 2cm.
d) Đặt tên giao điểm của hai đường tròn là C, D.
e) Vẽ đoạn thẳng CD.
g) Đặt tên giao điểm của AB và CD là I.
h) Đo IA và IB.
Vẽ lại các hình sau (cho đúng kích thước như hình đã cho).
Vẽ hình liên tiếp theo cách diễn đạt sau
a) Vẽ đoạn thẳng AB = 2cm. Vẽ đường tròn (C1) tâm A, bán kính AB.
b) Vẽ đường tròn (C2) tâm B, bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn (C1) là C và G.
c) Vẽ đường tròn (C3) tâm C, bán kính AC. Goi giao điểm mới củađường tròn này với đường tròn (C1) là D.
d) Vẽ đường tròn (c4) tâm D, bán kính AD. Gọi giao điểm mới của đường tròn này với đường tròn (c1) là E.
e) Vẽ đường tròn (C5) tâm E, bán kính AE. Gọi giao điểm mới của đường tròn này với đường tròn (C1) là F
f) Vẽ đường tròn (C6) tâm F, bán kính AF.
g) Vẽ đường tròn (C7) tâm G, bán kính AG.
Sau khi vẽ như trên hãy so sánh các đoạn thẳng: AB, BC, CD, DE, EF, FG, GB
Vẽ đường tròn tâm O, bán kính R = 3cm.Vẽ một đường kính AB. Vẽ tiếp một dây cung CD (hai điểm C, D không trùng với các điểm A,B và ba điểm C, O, D không thẳng hàng)
a) Đọc tên các cung có các đầu mút là hai trong số các điểm A, B, C, D.
b) So sánh độ dài của hai dây AB và CD.
c) Nếu lấy n điểm (phân biệt) trên đường tròn đó ta có được bao nhiêu cung
Lấy ba điểm A, B, C bất kỳ, không thẳng hàng.
Vẽ các đoạn thẳng AB, BC, CA.
a) Dùng compa để dựng đoạn MP = AB + BC
b) Dùng compa để so sánh AC với AB + BC
Cho 4 điểm A, B, C, D trong đó 3 điểm A, B, C thẳng hàng.
a) Vẽ tất cả các tam giác có đỉnh là 3 trong 4 điểm A, B, C, D;
b) Với các tam giác có được, hãy điền vào bảng sau:
Cho 4 điểm A, B, C, D trong đó không có 3 điểm nào thẳng hàng. Tính số tam giác có ba đỉnh là 3 trong 4 điểm trên. Viết tên các tam giác đó.
Tính số tam giác có được trong hình bên. Viết tên các tam giác đó.
Vẽ hình theo cách diễn đạt bằng lời sau: Vẽ ΔABC . Lấy M là điểm trong của ΔABC. Vẽ các tia AM, BM, CM cắt các cạnh của ΔABC tương ứng tại các điểm N, P, Q. Vẽ ΔNPQ. Hỏi điểm M có nằm trong ΔNPQ hay không?
a) Vẽ ∆EDF biết ED = 5 cm, EF = 4 cm, DF = 4 cm
b) Vẽ ∆PMU biết PM = 4 cm, MU = 4 cm, PU = 4 cm
c) Vẽ ∆ART biết AR = 5 cm, RT = 4 cm, AT = 3 cm
d) Mỗi tam giác trên có gì đặc biệt?
Vẽ hình để thấy được mỗi câu sau đây là sai
a) Hình gồm 3 đoạn thẳng được gọi là tam giác
b) Hình gồm 3 đoạn thẳng đôi một cắt nhau được gọi là tam giác.
c) Hình gồm 3 đoạn thẳng đôi một cắt nhau tạo ra 3 giao điểm (phân biệt) được gọi là tam giác.
d) Hình gồm 3 đoạn thẳng AB, BC, CA được gọi là tam giác ABC.
e) Hình gồm 3 điểm không thẳng hàng A, B, C được gọi là tam giác ABC.
f) Một điểm không thuộc cạnh của tam giác ABC thì phải là đỉnh của tam giác đó.
g) Một điểm không phải là đỉnh của tam giác ABC thì phải nằm trong tam giác đó.
h) Một điểm không nằm bên trong tam giác ABC thì phải nằm ngoài tam giác đó.
i) Hình gồm 2 góc được gọi là tam giác.
j) Hình gồm 3 góc mà các cạnh của nó đôi một cắt nhau tạo ra ba điểm được dọi là tam giác.
Vẽ hình liên tiếp theo cách diễn đạt sau đây
a) Vẽ tam giác ABC, có AB = 6cm, BC = 6cm, CA = 6cm.
b) Vẽ tiếp các điểm M, N, P tương ứng là trung điểm của các đoạn thẳng AB, BC, CA
c) Vẽ tiếp tam giác MNP.
d) Đọc tên, các góc, các cạnh của những tam giác có 3 đỉnh lấy trong số các điểm A, B, C, M, N, P.
a) Vẽ tam giác ABM có AB = 5cm, BM = AM = 6,5cm;
b) Vẽ tiếp góc Amx kề bù với góc AMB
c) Vẽ tam giác AMC, sao cho MA = MC và điểm C thuộc tia Mx;
d) So sánh MB, MA, MC;
e) Cho biết độ dài của đoạn thẳng BC;
f) Đo và cho biết số đo của góc BAC;
g) Đo và cho biết độ dài của đoạn thẳng AC
Cho nửa mặt phẳng bờ là đường thẳng a và 3 điểm M, N, P (phân biệt). Nếu hai điểm M, N khác phía với đường thẳng a và hai điểm N, P.
(A) khác phía với đường thẳng a thì hai điểm M, P khác phía với đường thẳng a;
(B) cùng phía với đường thẳng a thì hai điểm M, P cùng phía với đường thẳng a;
(C) cùng phía với đường thẳng a thì hai điểm M, P khác phía với đường thẳng a;
(D) cùng phía với đường thẳng a thì đôi một trong số các điểm M, P, N khác phía so với đường thẳng a.
Số góc có trong hình được tạo bởi 6 tia phân biệt, chung gốc bằng
(A) 5;
(B) 6;
(C) 15;
(D) 30.
Biết rằng \(\widehat {MNP} = {180^0}\), câu nào sau đây không đúng
(A) Ba điểm M, N, P thẳng hàng;
(B) Hai tia MP và MN đối nhau;
(C) Hai tia NP và NM đối nhau;
(D) MNP là góc bẹt.
Vẽ \(\widehat {mOn} = {36^0}\). Vẽ tiếp góc nOp kề bù với góc nOm. Vẽ tiếp góc pOt phụ với góc mOn và tia Ot ở trong góc pOn (h.bs.6). Khi đó, số đo của góc nOt bằng bao nhiêu?
(A) 54°
(B) 72°
(C) 90°
(D) 144°.
Vẽ \(\widehat {mOn} = {64^0}\). Vẽ tiếp góc nOp kề bù với góc nOm. Vẽ tiếp Ox là tia phân giác của góc mOn. Vẽ tiếp Oy là tia phân giác của góc pOn (h.bs.7). Khi đó, số đo của góc xOy bằng bao nhiêu?
(A) 90°;
(B) 58°;
(C) 36°;
(D) 116°.
Vẽ \(\widehat {mOn} = {100^0}\) (h.bs.8). Vẽ tiếp \(\widehat {mOX} = {90^0}\) và tia Ox ở trong góc mOn. Vẽ tiếp \(\widehat {mOY} = {10^0}\) và tia Oy ở trong góc mOn. Vẽ tiếp Oz là hai tia phân giác của góc mOn. Khi đó số đo của góc xOz bằng bao nhiêu?
(A) 10°;
(B) 40°;
(C) 50°;
(D) 80°.
Biết rằng hai góc mOn và nOp kề bù, hơn nữa \(\widehat {mOn} = 5\widehat {nOp}\). Khi đó
(A) \(\widehat {mOn}\) = 30° và \(\widehat {nOp}\) = 150°;
(B) \(\widehat {mOn}\) = 150° và \(\widehat {nOp}\) = 30°;
(C) \(\widehat {mOn}\) = 144° và \(\widehat {nOp}\) = 36°;
(D) \(\widehat {mOn}\) = 36° và ∠\(\widehat {nOp}\) = 144°.
Trên đường tròn tâm O bán kính R (R > 0) lấy 5 điểm M, N, P, Q, S. Khi đó, số các cung có hai đầu mút lấy trong số các điểm đã cho bằng
(A) 20;
(B) 10;
(C) 40;
(D) 200
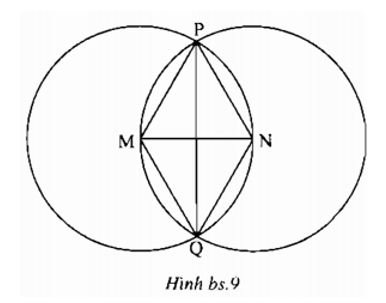
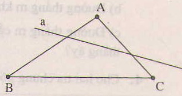
Cho hình bs.9. Khi đó
(A) MP = MQ = MN = PQ;
(B) MP = MQ = NQ = NP;
(C) MP = MQ = NP = PQ;
(D) MP = MQ > NQ = NP;
Tam giác MNP có MP = 6cm, MN = PN = 5cm. Góc MNx kề bù với góc MNP. Điểm Q trên tia Nx sao cho NQ = NM (h.bs.10). Khi đó, độ dài của đoạn thẳng PQ bằng
(A) 5;
(B) 6;
(C) 8;
(D) 10.
Copyright © 2021 HOCTAP247