Bài tập 23 trang 87 SBT Toán 6 Tập 2
Bài tập 23 trang 87 SBT Toán 6 Tập 2
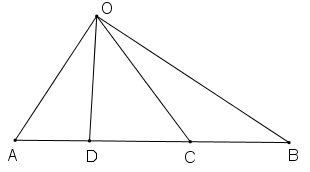
Trên đường thẳng d từ trái sang phải ta lấy các điểm A, D, C, B và lấy điểm O nằm ngoài đường thẳng d.
Biết: \(\widehat {AOD} = {30^0}\), \(\widehat {DOC} = {40^0}\); \(\widehat {AOB} = {90^0}\). Tính \(\widehat {AOC},\widehat {COB},\widehat {DOB}\)
Vì D nằm giữa A và C nên tia OD nằm giữa hai tia OA và OC.
Suy ra: \(\widehat {AOC}\) = \(\widehat {AOD}\) + \(\widehat {DOC}\) = 300 + 400 = 700
Vì C nằm giữa A và B nên tia OB nằm giữa hai tia OA và OB.
Suy ra: \(\widehat {AOB}\) = \(\widehat {AOC}\) + \(\widehat {COB}\)
=>\(\widehat {COB}\) = \(\widehat {AOB}\) - \(\widehat {AOC}\) = 900 - 700 = 200
Vì D nằm giữa A và B nên tia OD nằm giữa hai tia OA và OB.
Suy ra: \(\widehat {AOB}\)) = \(\widehat {AOD}\) + \(\widehat {DOB}\)
=>\(\widehat {DOB}\)= \(\widehat {AOB}\) - \(\widehat {AOD}\) = 900 - 300 = 600
-- Mod Toán 6
Copyright © 2021 HOCTAP247